A particle moves along Y - axis from y = 0 m under the influence of a force F=(9+3y+5y)2 N . Calculate the work done on the particle .
To solve the problem of calculating the work done on a particle moving along the Y-axis under the influence of the force F=(9+3y+5y2)N, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done dW by a force F when moving a particle through a small displacement dy is given by:
dW=F⋅dy
Step 2: Substitute the Given Force
We substitute the expression for the force into the work done formula:
dW=(9+3y+5y2)dy
Step 3: Integrate to Find Total Work Done
To find the total work done W as the particle moves from y=0 to y=Y, we integrate dW:
W=∫Y0(9+3y+5y2)dy
Step 4: Perform the Integration
Now we perform the integration term by term:
1. The integral of 9 with respect to y is:
∫9dy=9y
2. The integral of 3y with respect to y is:
∫3ydy=3y22
3. The integral of 5y2 with respect to y is:
∫5y2dy=5y33
Combining these results, we have:
W=(9y+3y22+5y33)Y0
Step 5: Evaluate the Integral from 0 to Y
Now we evaluate the expression from 0 to Y:
W=(9Y+3Y22+5Y33)−(9⋅0+3⋅022+5⋅033)
Since the second part is zero, we have:
W=9Y+3Y22+5Y33
Final Result
Thus, the work done on the particle as it moves from y=0 to y=Y is:
W=9Y+3Y22+5Y33Joules
The work done dW by a force F when moving a particle through a small displacement dy is given by:
dW=F⋅dy
We substitute the expression for the force into the work done formula:
dW=(9+3y+5y2)dy
To find the total work done W as the particle moves from y=0 to y=Y, we integrate dW:
W=∫Y0(9+3y+5y2)dy
Now we perform the integration term by term:
1. The integral of 9 with respect to y is:
∫9dy=9y
2. The integral of 3y with respect to y is:
∫3ydy=3y22
3. The integral of 5y2 with respect to y is:
∫5y2dy=5y33
W=(9y+3y22+5y33)Y0
Now we evaluate the expression from 0 to Y:
W=(9Y+3Y22+5Y33)−(9⋅0+3⋅022+5⋅033)
Since the second part is zero, we have:
W=9Y+3Y22+5Y33
Thus, the work done on the particle as it moves from y=0 to y=Y is:
W=9Y+3Y22+5Y33Joules
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - PRACTICE PROBLEMS
27 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions
20 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Knowledge Check
A particle moves along X-axis from x=0 to x=1 m under the influence of a force given by F=3x2+2x−10. Work done in the process is
A+4JB−4JC+8JD−8JA particle moves along the X-axis x=0 to x=5 m under the influence of a force given by F=10−2x+3x2. Work done in the process is
A70 unitsB270 unitsC35 unitsD150 unitsA particle moves along x -axis under the action of a position dependent force F =(5x2−2x)N. Work done by forces on the particle when it moves from origin to x=3m is
A45JB36JC32JD42J
A particle moves along the X-axis from x=0 to x=5 m under the influence of a force given by F=7−2x+3x2. Find the work done in the process.
View SolutionA particle moves under the effect of a force F=kx2 from x=0 to x=4, the work done by force is ?
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by
F=7−2x+3x2. The instantaneous power applied to the particle is.
View SolutionA particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
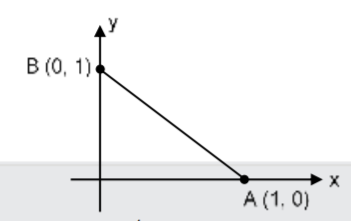
View Solution
