Complete Solutions to SOLVED EXAMPLES of chapter OSCILLATIONS AND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| PRADEEP | SOLVED EXAMPLES |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
A particle executes SHM given by `y=0.24sin(400t+0.5)` in SI units. Find `(i)` amplitude `(ii)` frequency and `(iii)` time period of vibration.
01:32View SolutionA particle executes SHM with a time period of `4 s`. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
02:22View SolutionA body oscillates with SHM, accroding to the equation, `x=(5.0m)cos[(2pi t+pi//4]`
At `t=1.5s`, calculate the `(a)` diplacement `(b)` speed and `(c)` acceleration of the body.09:01View SolutionA particle executed SHM iwht a time period of 3s and amplitude 6cm. Find (i) displacement (ii) velocity and (iii) acceleration, after `1//2` second, starting from the mean position.
02:55View SolutionA particle moving in a straight line has velovity v given by `v^(2)=alpha-betay^(2)` , where `alpha` and `beta` are constants and y is its distance from a ficed point in the line. Show that the motion of particle is SHM. Find its itme period and amplitude.
03:16View SolutionThe equations of simpel harmonic motin is given by
`y=3sin5pit+4cos5pit`, where y is in cm and t in second. Determing the amplitude, period and initial phase.02:02View SolutionA particle executed SHM o amplitude 20cm and itme period 4s. What is minimum time required for the particle to move between two points 10cm on either side of mean position?
02:15View SolutionA particle executing SHM along a straight line has a velocity of `4ms^(-1)`, and at a distance of 3m from its mean position and `3ms^(-1)`, when at a distance of 4m from it. Find the time it take to travel 2.5m from the positive extremity of its oscillation.
10:42View SolutionA man stands on a weighing machin palced on a horizontal platform the machine reads 50kg. By mean of a suitable mechanism, the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibration per second. What will be the effect on the readin of the weighing machin? Teh amplitude of vibration of platform is 5cm. Take `g=10ms^(-1)`
02:59View SolutionA particle executes simple harmonic motion with a time period of 16s. At time `t=4s` its velocity is `4ms^(-1)`. Find its amplitute of motion.
03:14View SolutionThe displacement `y` of a particle executing periodic motion is given by `y = 4 cos^(2) ((1)/(2)t) sin(1000t)`
This expression may be considereed to be a result of the superposition of02:36View Solutiondepict two circulat mothions. The radius of the circle, the period of revolution, the initial position and sense of revolution are indicated in the figures. Obtain the simple harmonic motinosof the x-projection of the radius vector of the rotating particle P in each case.
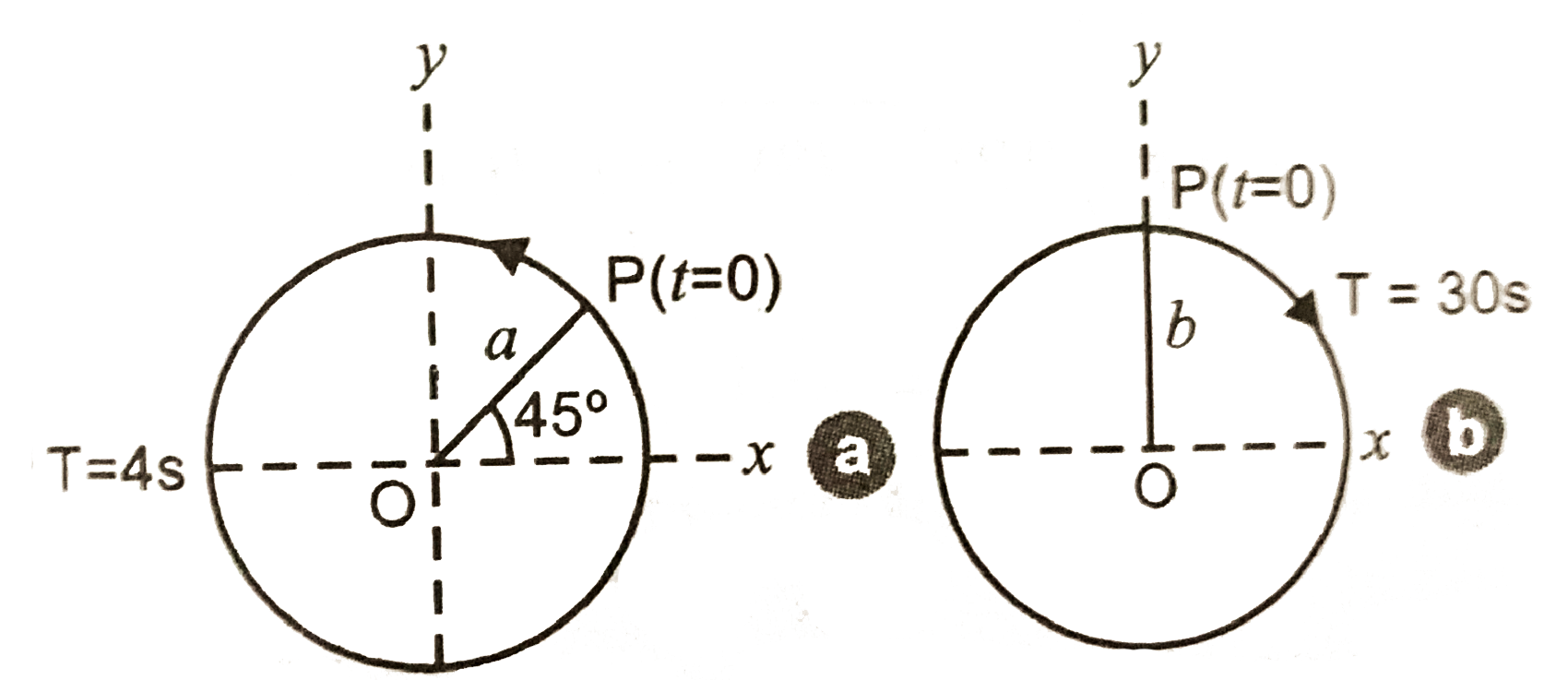 06:04View Solution
06:04View SolutionTime period of a simple pendulum is 2s and it can go to and fro from equilibrium position at a maximum distance of 6cm. If at the start of the motion the pendulum is in the position of maximum displacement towards the right of the equilibrium position, then write the displacement equation of the pendulum.
02:18View SolutionMaximum velocity of a particle in SHM is `16cm^(-1)` . What is the average velocity during motion from one extreme position to other extreme position?
02:35View SolutionA block of mass one kg is fastened to a spring with a spring constant `50Nm^(-1)`. The block is pulled to a distance `x=10cm` from its equilibrium position at `x=0` on a frictionless surface from rest at `t=0. ` Write the expression for its x(t) and v(t).
02:30View SolutionA body executed SHM of time period 6s. If its mass be 0.1kg, its velocity, 1s after it passes throuh mean position be `3ms^(-1)`, find its (i) KE (ii) PE and (iii) total energy.
03:24View SolutionA particle of mass 100g is dexcribing SHM along a straight lig with a period of 2s and amplitude of 12 cm. What is the knetice energy when it is (i) 3cm (ii) 6cm from its equilibrium position? `(Use pi^(2)=10)`
02:50View SolutionA mass of 1 kg is executing SHM which is give by, `x=6.0cos(100t+pi//4)`cm. What is the maximum kinetic energy?
01:34View SolutionAn 8kg body performs SHM of amplitude 30cm. The restoring fore is 60n, when the displacement is 30cm. Find (a) time period (b) the acceleration, P.E and K.E., when displacement is 12 cm.
05:47View SolutionA point particle if mass `0.1 kg` is executing SHM of amplitude `0.1 m`. When the particle passes through the mean position, its kinetic energy is `8 xx 10^(-3)J`. Write down the equation of motion of this particle when the initial phase of oscillation is `45^(@)`.
02:16View SolutionA linear harmonic oscillator of force constant `2 xx 10^6 N//m` and amplitude (0.01 m) has a total mechanical energy of (160 J). Its.
03:45View SolutionA small trolley of mass 2.0kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation at a speed of 360 rpm,, the length of the stretched spring is 43cm. If the original length of the spring is 36cm, determing the force constant of the spring.
02:17View SolutionA period of oscillation of a mass m kg is suspended by an ideal spring is 1.5s. If an additional mass 3kg be suspended, the time period is increased by 1s. Find the value of m.
02:44View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.
 02:35View Solution
02:35View SolutionTwo identical springs, each of force constant k are connected I `(a)` series `(b)` parallel and they support a mass M. Calculate the ratio of the frequency of oscillation of the mass in two systems.
02:17View SolutionA small trolley of mass 2.0kg resting on a horizontal turn table is connected by a light spring to the centre of the table. When the turn table is set into rotation a speed of 600rpm, the length of stretched spring is 50cm. If the original length of the spring is 42cm, find the force constant of the spring.
02:42View SolutionA block whose mass is 1 kg is fastened to a spring.The spring has a spring constant `50Nm^(-1)`. The block is pulled to a distance `x=10cm` from its equilibrium position at `x=0` on a frictionless surface at `t=0`. Calculate the kinetic, potential and total energies of the blocak when it is 5cm away from the mean position.
02:11View SolutionA spring of force constant `1200Nm^(-1)` is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released , what is
(a) the speed of the mass when the spring is compressed by 1.0cm?
Potential energy of the mass when it momentarily comed to rest ?
(c) Total energy of the oscillating mass.
 05:12View Solution
05:12View SolutionA tolley of mass 3.0kg is connected to two identical spring each of force constant `600Nm^(-1)` as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?
 05:44View Solution
05:44View SolutionA 5 kg colloar is attached to a sprinig of spring constatn 500`Nm^(-1)` . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by oscillations (b) The maximum speed and © maximum acceleration of the collar.
01:58View SolutionA solid cylinder of mass `m` is attached to a horizontal spring with force constant `k`. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period `T = 2pisqrt((3m)/(2k))`, if displaced from mean position.
 03:36View Solution
03:36View SolutionIf the length of simple pendulum is increased by `50%`, what is the percentage increase in its time period?
01:41View SolutionA pendulum clock nnormally shows correct time. On an extemely cold day, its length decreases by `0.2%`. Compute the error in time per day.
03:24View SolutionA second pendulum is takin in a carriage. Find the period of oscillation when the carriage moves with an acceleration of `4*2ms^(-2)` (i) vertically upwards (ii) vertically downwards and (ii) in a horizontal direction.
05:06View SolutionA body is droppped in a hole drilled across a diameter of the earth. Show that it executes SHM. Assume the earth to be homogenous sphere.
02:04View SolutionA sphere is hung with a wire, `45^(@)` rotation of th esphere about the wiere generates a restoring torque of 6.0Nm. If the moment of inertia of the sphere is `0.080kgm^(2)`, deduce the frequency of angular oscillations.
02:21View SolutionA simple pendulum has time period (T_1). The point of suspension is now moved upward according to the relation `y = K t^2, (K = 1 m//s^2)` where (y) is the vertical displacement. The time period now becomes (T_2). The ratio of `(T_1^2)/(T_2^2)` is `(g = 10 m//s^2)`.
02:32View SolutionTwo particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is one thhird their amplitude. What is the phase difference between them?
09:00View SolutionTwo simple pendulums of lengths 1.21m and 1.00 m start swinging at the same time from a location. After how much time, they will be (a) out of phase and (b) in phase again? Take `g=10m//s^(2)`.
09:46View SolutionFor the damped oscillatore shown in figure., the mass m of the block is 200g, `K=90Nm^(-1)` and the damping constant b is `40gs^(-1)`. Calculate (a) the period of oscillation, (b) time taken for its amplitude of vibrations to drop to half of its initial value of (c) the itme taken for its mechanical energy to drop to half its inital value.
View SolutionSprings of spring constants k, 2k, 4k, 8k, …… are connected in series. A mass m kg is attached to the lower end of the last spring and the systemm is allowed to vibrate. What is the time period of oscillations? Given `m=40gm,k=2.0Ncm^(-1)`.
02:02View SolutionHow far does the sound travel in air, when a tuning fork of frequency 256 Hz makes 32 vibrations? Velocity of sound in air `=320m//s`.
01:11View SolutionThe speed of a wave in a mediium is `960ms^(-1)`. If 3600waves are passing through a point in medium in 1 minute. What is the wavelength of waves?
00:58View SolutionIn a sonometer experiment, the density of material of the wire used in `7.5xx10^(3)kg//m^(3)`. If the stress of the wire is `3.0xx10^(8)N//m^(2)`, find out the speed of transvers waves in the wire.
02:03View SolutionA wave pulse is travelling on a string of linear mass density `10gcm^(-1)` under a tension of 1kg wt. Calculate the time taken by the pulse to travel a distance of 50cm on the string. Take `g=10m//s^(2).`
01:43View SolutionAt a pressure of `10^(5)N//m^(2)`, the volumetric strain of water is `5xx10^(-5)`. Calculate the speed of sound in water. Density of water is `10^(3)kg//m^(3).`
01:36View SolutionIf the splash is hear 4.23 seconds after a stone is dropped into a well, 78.4 metres deep, find the velocity of sound in air.
02:11View SolutionA steel wire 70cm long has a mass of 7.0g. If the wire is under a tension of 100N, what is the speed of transverse waves in the wire?
01:45View SolutionEstimate the speed of sound in air at standard temperature and pressure. The mass of 1 mole of air is `29.0xx10^(-3)kg`, `lambda` for air `=7//5`.
02:22View SolutionAt what temperature will the speed of sound be double its value at 273K?
01:14View SolutionAt normal temperature and pressure, the speed of sound in air is 332 m`//`s. What will be the speep of sound in hydrogen at `546^(@)C` and 2 atmospherica pressure ? Given air is 16 times heavier than hydrogen.
03:37View SolutionThe ratio of densities of oxygen and nitrogen is 16`:`14. At what temperature, the speed of sound in oxygen will be equal to its sped in nitrogen at `14^(@)C`?
02:14View SolutionWhat is the ratio of velocity of sound in hydrogen `(gamma=7//5)` to that in helium `(gamma=5//3)` at the same temperature?
01:40View SolutionFind the temperature at which sound travels in hydrogen with the same velocity as in ocygen at `1000^(@)C`. Density of oxygen is 16times that of hydrogen.
03:35View Solution
SOLVED EXAMPLES questions and complete solutions for chapter OSCILLATIONS AND WAVES of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS OSCILLATIONS AND WAVES
- Additional Exercises
- Advanced Problems For Competitions
- Assertion-Reason Type Questions
- conceptual problems
- CURIOSITY QUESTION
- Fill In The Blanks
- Higher Order Thinking Skills
- integer type question
- JEE mains adv..(multiple choice quection)
- Long Answer Questions
- Multiple Choice Question
- Multiple Choice Question-I
- Multiple Choice Question-II
- multiple choice Questions
- NCERT CHAPTER
- NCERT EXERCISES WITH SOLUTIONS
- PROBLEMS FOR PRACTICE
- SAMPLE PROBLEM
- Short Answer Questions
- SOLVED EXAMPLES
- Value Based Questions
- Very Short Answer Questions
