Complete Solutions to SAMPLE PROBLEM of chapter OSCILLATIONS AND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| PRADEEP | SAMPLE PROBLEM |
| Number Of Questions | 71 |
| Academic Year | 2023-24 |
A particle executes SHM with a time period of 2s and amplitude 5 cm. Find (i) displacement (ii) velocity (iii) acceleration, after `1//3` second, starting from mean position.
03:08View SolutionA partical executes SHM on a straigh line path. The amplitude of oscillation is 2cm. When the displacement of the particle from the mean position is 1cm, the magnitude of its acceleration is equal to that of its velocity. Find the time period of SHM, also the ms. velocity and ms. acceleration of SHM.
02:20View SolutionA body weighing 10 kg is executing SHM, has a velocity of `6.0ms^(-1)`, after one second of starting from the mean position. If its time period is 6 second, find its K.E., P.E. and total energy.
08:26View SolutionThe total energy of a partical executing simple harmonic motion of period `2pi` secon is 10,240ert. The displacement of the particle at `pi//4` second is `8sqrt(2)cm`. Calculate the amplitutde of motion and mass of the particle
03:01View SolutionWhat will be the time period of second's pendulumm if its length is doubled?
01:03View SolutionThe acceleration due to gravity on the surface of the moon is `1.7ms^(-2)`. What is the time perioid of a simple pendulum on the surface of the moon, if its time period on the surface of earth is `3.5s ?` Take `g=9.8ms^(-2)` on the surface of the earth.
01:53View SolutionA vertical U tube of uniform cross-section contains water up to a heigth of `0.5m` . If water on one side is depressed a little and then released its motino up and down the two sides of the tube is SHM. Calculate (i) time period (ii) angular grequency of vibration. ` g=10ms^(2)`.
01:35View SolutionA cubical body (side `0.1m` and mass `0.002kg)` floats in water. It is pressed and then released so that it executes SHM. Find the time period. `(g=10m//s^(2))`
04:50View SolutionA spring compressed by `0.1`m develips a restoring force 10N. A body of mass 4kg is placed on it. Deduce `(i)` the force constant of the spring `(ii)` the depression of the spring under the weight of the body `(` take `g=10N//kg)` and `(iii)` the period of oscillation, if the body is left free.
01:58View SolutionA mass m attached to a spring oscillates with a period 2s. If the mass is increased by 2kg, the period increases by 1s. Find the initial mass m, asssuming that Hooke's law is obeyed.
01:47View SolutionA transverse harmonic wave on a string is described by `y(x,t)=3.0sin(36t+0.018x+pi//4)` where x, y are in cm, t in second. The positive direction of x is from left to right . (i) Is this a travelling or stationary wave ? If travellying, what are the speed and direction of its propagation ? (ii) what are its amplitude and frequency ? (iii) what is the inital phase at the origing ? (iv) What is the least distance between two successive creests in the wave?
07:38View SolutionA simple harmonic wave train of amplitude 1 cm and frequency 100 vibration is travelling along positive x-direction with a velocity of `15ms^(-1)`. Calculate displacement y , the particle velocity and particle acceleration at `x=180cm` from the origin at `t=5` s.
04:29View SolutionFigure shows a string of linear mass density `1.0g cm^(-1)` on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of `50 cm` on the string. Take `g = 10 ms^(-2)`
 01:12View Solution
01:12View SolutionA tuning fork of frequency 220Hz produces sound waves of wavelength 1.5m in air at NTP. Calculate the increase ini wavelenth, when temperature of air in `27^(@)C`.
02:54View SolutionA wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45Hz. The mass of the wire is `3.5xx10^(-2)` kg and its linear density is `4xx10^(-2)` kg`//`m . What is the speed of transverse wave on string and tension in the wire?
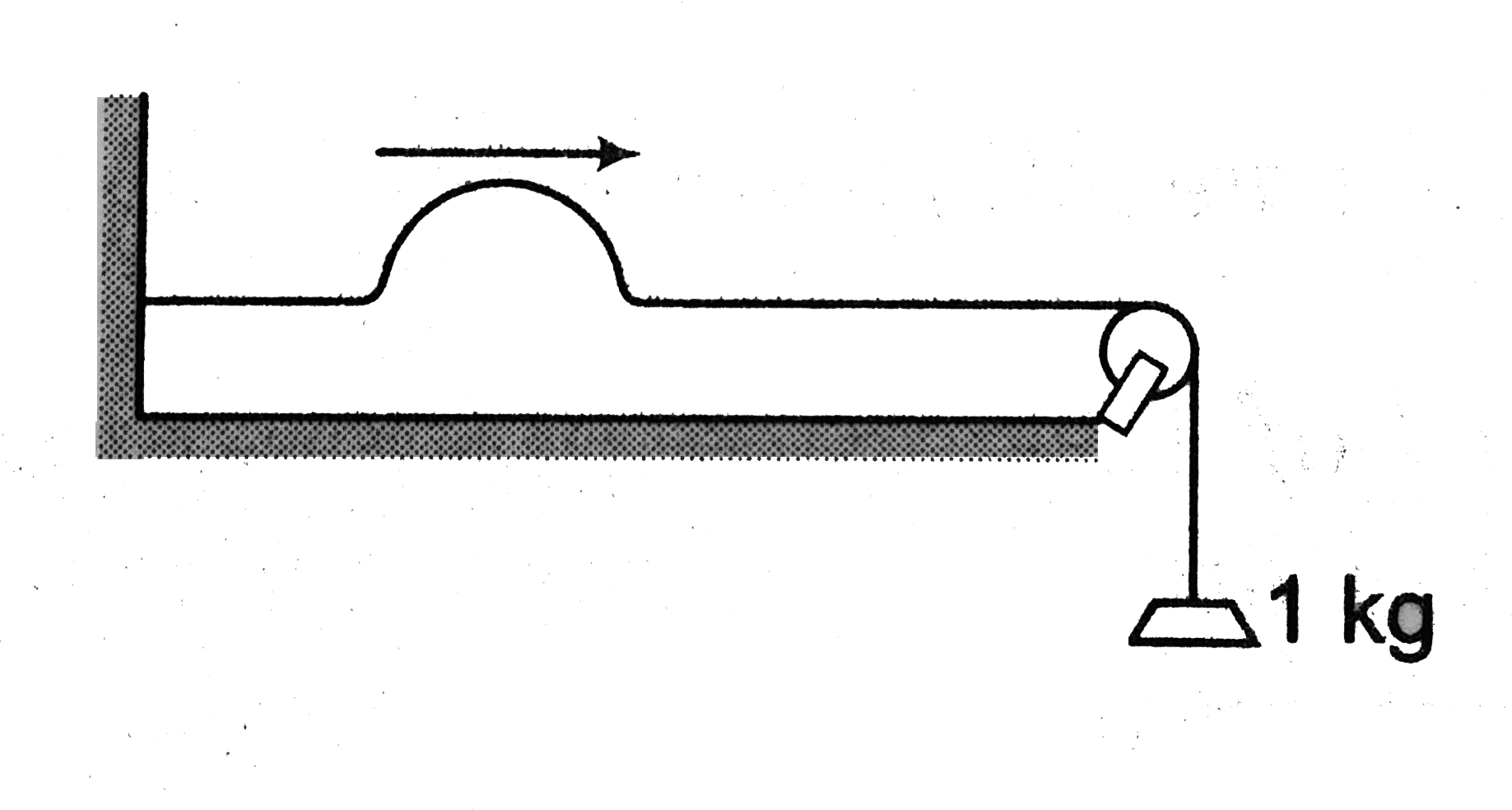
03:18View SolutionA 100 cm long wire of mass 40 g supports a mass of 1.6 kg as shown in figure . Find the fundamental frequency of the portion of the string between the wall and the pulley. Take `g=10m//s^(2)`.
 02:48View Solution
02:48View SolutionA pipe 20cm long is closed at one end. Which harmonic mode of th epipe is resonantly excited by a 430Hz source? Will the same source be in resonance with the pipe if both ends are open? Take speed of sound in air `340m//s`.
03:10View SolutionA tuning fork of frequency 200Hz is in unison with a sonometer wire. How many beats`//`sec will be heard if tension in the wire is increased by `2%`?
02:38View SolutionA siren is fitted on as car going towards a vertical wall at a speed of 36 km/h. A person standing on the ground, behind the car, listens to the siren sound coming directly from the source as well as that coming after refelction from the siren to the person and b. coming after reflection. Take the speed of sound to be `340ms^-1`
04:16View SolutionThe speed of sound in dry air at NTP is 332 metres `//`sec. Assuming air as composed of 4 parts of nitrogen and one part of oxygen, calculate velocity of sound in ocygen under similar condistions, when the densities of oxygen and nitrogen at NTP are in the ration of `16:14` respectively .
03:40View SolutionCalculate the temperature at which sound travels in hydrogen with the same speed as in helium at N.T.P. The density of helium is twice that of hydrogen.
01:46View SolutionA wave on a string is described by `y(x,t)=0.005sin(6.28x-314t)`, in which all quantities are in SI units. Calculate its amplitude and wavelength.
01:12View SolutionThe displacement of a particle in a medium can be expressed as
`y=10^(-6)sin(100t+20x+pi//4),`
where x is in metre and t is in second. What is the speed of the wave?01:33View SolutionA transverse harmonic disturbance is produced in a string. The maximum transverse velocity is `3m//s` and maximum transverse acceleration is `90m//s`. If the wave velocity is `20 m//s` then find the waveform.
02:57View SolutionFor a travelling haromonic wave , `y=2.0cos(10t-0.0080x+0.818)` where x and y are in cm and t is in sec. What is the phase difference between two points separated by (i) a distance of 0.5m (ii) time gap of 0.5s.
02:58View SolutionA displacement wave is represented by
`xi=0.25xx10^(-3)sin(500t=0.025x)`
Deduce (i) amplitude (ii) period (iii) angular frequency (iv)wavelength (v) amplitude of particle velocity (vi) amplitude of particle acceleration . `xi`, t and x are in cm, sec, and metre respectively.03:51View SolutionA wave travelling along a strong is described by
`y(x,t)=0.005 sin (80.0x-3.0t)`
in which the numerical constants are in SI units `(0.005m, 80.0 rad m^(-1)` and `3.0 rad s^( -1))`. Calculate (a) the amplitude. (b) the wavelength (c) the period and frequency of the wave. Also , calculate the displacement y of the wave at a distance `x=30.0` cm and time t=20 s?02:37View SolutionA simple harmonic wave train of amplitude 1 cm and frequency 100 vibration is travelling along positive x-direction with a velocity ov `15ms^(-1)`. Calculate displacement y , the particle velocity and particle acceleration at `x=180cm` from the origin at `t=5` s.
04:29View SolutionThe equation of a plane progressive wave is give by equation
`y=10sin2pi(t-0.005x)`
where y and x are in cm and t is in seconds. Calculate the amplitude, frequency, wavelength and velcoity of the wave.02:20View SolutionA wave is expressed by the equation
`y=0.5sinpi(0.01x-3t)`
where y and x are in metre and t in seconds. Find the speed of propagation.01:57View SolutionThe distance between two consecutive nodes in a stationary wave is 25cm. If the speed of the wave is `250ms^(-1)`, calculate the frequency.
01:05View SolutionA stationary wave is described by the equation `y=10sin(x//3)cos(15pit),` where x is in cm and time t is in second. Calculate frequency and velocity of component waves. Also, find the amplitude of stationary waves at antinodes and find the position of first antinode.
06:07View SolutionWrite the equation of a wave identical to the wave represented by the equation `y=5sinpi(4.0t-0.02x)`, but moving in opposite direction. Write the equation of stationary wave produced by the combination of these two waves. Determine the distance between two nearest nodes. All distances in the equations are in mm.
05:46View SolutionTwo travalling wavews of equal amplitudes and equal frequencies move in opposite directions along a string. They interfere to produce a standing wave having the equation `y = A cos kx sin omega t` in which `A = 1.0 mm, k = 1.57 cm^(-1) and omega = 78.5 s^(-1)` (a) Find the velocity of the component travelling waves. (b) Find the node closet to the origin in the x gt 0. (c ) Find the antinode closet to the origin in the region x gt 0 (d) Find the amplitude of the particle at x = 2.33cm.
09:04View SolutionThe following equation represents standing wave set up in a medium ,
`y = 4 cos (pi x)/(3) sin 40 pi t`
where `x and y` are in cm and t in second. Find out the amplitude and the velocity of the two component waves and calculate the distance adjacent nodes . What is the velocity of a medium particle at ` x = 3 cm` at time `1//8 s`?05:13View SolutionCalculate the fundamental frequency of a sonometer wire fo length 20cm, tension 25N, cross sectional area `10^(-2)cm^(2)` and density of material `=10^(4)kg//m^(3)`.
02:11View SolutionA stretched wire emits a fundamental note of frequency 256Hz. Keeping the stretchin force constant and reducing the length of the wire by 10cm, frequency becomes 320Hz. Calculate original length of the wire.
03:31View SolutionA string vibrates in three loops when 8gram weight is placed in the pan. What mass should be kept in the pan to make it vibrate in six loops. Neglect the mass of string and mass of pan.
02:32View SolutionA sonometer wire has a length of 114 cm between its two fixed ends. Where should the two briges be places so as todivide the wire into three segments, whos fundamental frequencies are in the ratio `1:3:4?`
02:53View SolutionAwire having a linear mass density of `5.0xx10^(-3)kgm^(-1)` is stretched between two rigid supports with a tension of 45N. The wire resonates at a frequency of 420Hz. The next higher frequency at which the wire resonates is 490Hz. Find the length of the wire.
02:02View SolutionFind the fundamental note emitted by a string of length `10sqrt(10)` cm under tension of 3.14 kg. Radius of string is 0.55 mm and density `=9.8gcm^(-3)`.
04:48View SolutionA wire of density `9000 kg//m^(3)` is stretched between two clamps `100 cm` apart while subjected to an extension od `0.05 cm`. What is the lowest frequency of transverse vibrations in the wire , assuming Young's modulus of the material to be `9 xx 10^(10) N//m^(2)`?
03:22View SolutionThe length of a sonometer wire between two fixed ends is 110cm. Where should the two bridges the placed so as to divide the wire into three segments, whose fundamental frequencies are in the ration` 1:2:3?`
02:08View SolutionA stone hangs in air from one end of a wire, which is stretched over a sonometer. The wire is in unison with a certain tuning fork when the bridges of sonometer are 45 cm apart. Now the stone hangs immersed in water at `4^(@)C` and the distance between the bridges has to be altered by 9cm to re-establish unison of the wire with the same fork. Calculate the density of the stone.
08:01View SolutionFind the rationof the length of a closed pipe to that of an open pipe in order that the second overtone of the former is in unison with fourth overtone of the latter.
02:07View SolutionA well with vertical lsides and water at the bottom resonates at 7Hz and at no other lower freqency. The air in the well has density `1.10kgm^(-3)` and bulk modulus of water is `1.33xx10^(5)N//m^(2)`. How deep is the well ?
02:13View SolutionA tuning fork of frequency 341 Hz is vibrated just over a tube of length 1m. Water is being poured gradually in the tube. What height of water colume will be required for resonance?Speed of sound in air is 341 m `//` s.
02:31View SolutionThe fundamental tone produced by an organ pipe has a frequency of 110 Hz. Some other frequencies produced by the pipe are 20, 440, 550, 660 Hz. Is this pipe open or closed?Calculate effective length of the pipe. Speed of sound is 330m`//`s.
01:57View SolutionThe funadamental frequency of a closed organ pipe is equal to the first overtone frequency of an open organ pipe. If the length of the open pipe is 60 cm, what is the length closed pipe?
02:20View SolutionA pipe 30.0 cm long is open at both ends. Which harmonic mode of the pipe resonates with a 1.1kHz source? Will resonance with the same source be observed if one end of the pipe is closed ? Take the speed of sound in air as `330ms^(-1)`.
06:24View SolutionThird overtone of a closed organ pipe is in unison with fourth harmonic of an open organ pipe. Find the ratio of lengths of the two pipes.
02:00View SolutionA tuning fork of unknown frequency gives 4beats with a tuning fork of frequency 310 Hz. It gives the same number of beats on filing. Find the unknown frequency.
02:24View SolutionA tuning fork produces 4 beats`//`s when sounded with a fork of frequency 512 Hz. The same tuning fork. When sounded with another fork of frequency 514 Hz produces 6 beats `//` second. Find the unknown frequency of the fork.
02:10View SolutionIn an experiment, it was found that a tuning fork and sonometer wire gave 5 beats per second, both when the length of wire was 1m and 1.05m. Calculate the frequency of the fork.
02:54View SolutionA and B are two wires whose fundamental frequencies are 256 and 382 Hz respectively. How many beats in 2 seconds will be heard by the third harmonic of A and secondd harmonic of B?
01:25View SolutionAt `16^(@)C,` two open end organ pipes, when sounded together give 14 beats in 2 pipes, when sounded together give 14 beats in 2 seconds. How many beats per second will be produced if the temperature is raised to `51^(@)C` ? Neglect increase in length of the pipes.
05:11View SolutionTwo sitar strings A and B playing th note 'Dha' are slightly out of tune and produce beats of frequency 5hz. The tension of string B is slightly increased and the beat frequency is found to decrease to 3hz. What is th eoriginal frequency of B, if the frequency of A is 427 hz?
03:01View SolutionA set of 25 tuning forks is arranged in order of decreasing frequency. Each fork gives 3 beats with succeding one. The first fork is octave of the last. Calculate the frequency of the first and 16th fork.
02:53View SolutionTwo tunig forks A and B produce 6 beats `//` sec. On loading A with wax number of beats remains unaltered. However, when a little of wax is removed, the number of beats becomes 2 in 2 seconds. Calculate original frequency of A if that of B is 256.
02:52View SolutionThe identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to occurrence of 6 beats//s when both the wires oscillate together would be
01:09View SolutionAn observer moves towards a stationary source of sound, with a velocity one-fifth of the velocity of sound. What is the percentage increase in the apparent frequency?
02:30View SolutionAn observer standing on a railway crossing receives frequencies 2.2 kHz and 1.8 kHz when the tran approaches and recedes from the observer. Find the velocity of the train (speed of sound in air is 300 m/s).
02:30View SolutionAn observer is moving towards a wall at `2ms^(-1)`. He hears a sound from source at some distance behind him directly as well as after reflection from the wall. Calculate the beat freqecny between these two sound, if the true frequency of the source is 680 Hz. Velocity of sound `-340m//s`.
02:53View SolutionA policeman blos a whistle of frequency 400Hz as a car speeds past him with a velocity of `54km h^(-1)`. Find the cahnge in frequency as heard by the driver of the car just as he passes the policeman. Velocity of sound in air is `350ms^(-1)`
03:23View SolutionA rocket is moving at a speed of `200ms^(-1)` towards a stationary target. While moving, it emits a wave of frequency 1000hz. Some of the sound reaching the target gets reflected back to the racket as an echo. Calculate the frequency of sound as detected by the person at the position of tartget and frequecny of echo as detected by the rocket . Given velocity of soun `=330ms^(-1)`.
04:35View SolutionFind the diffference is the apparent frequencies (i) When the source approaches a stationary observer (ii) When observer is approaching the stationary source. Take b as relative velocity in each case and `upsilon` as the velocity of the waves.
02:57View SolutionA train moves towards a stationary observer with speed `34 m//s`. The train sounds a whistle and its frequency registered by the observer is `f_(1)`. If the train's speed is reduced to `17 m//s`, the frequency registered is `f_(2)`. If the speed of sound of `340 m//s`, then the ratio `f_(1)//f_(2)`is
04:06View SolutionA whistle is whirled in a circle of radius 1m with 7rps. An observer is situated outside the circle, but in its plane. If the speed of sound is 336`m//s`, find the interval between the highest and lowest observed pitches.
05:36View SolutionThe two parts of a sonometer wire divided by a movable knife edge , differ in length by `2 mm` and produce `1 beat//s` , when sounded together . Find their frequencies if the whole length of wire is `1.00 m`.
03:59View SolutionTwo tuning forks A and B give 9beats in 3 seconds. A resounds with a closed column of air 15cm long and B with an open column 30.5 cm long. Calculate their frequencies (neglect end correction).
04:17View SolutionA brass rod (density `8.3 g//cm^(3))`, 3m long is clamped at the centre. It is excited to give longitudinal vibrations and the frequency of the fundamental note is 600Hz. Calculate the velocity of sound in the rod and its Young's modulus.
02:09View Solution
SAMPLE PROBLEM questions and complete solutions for chapter OSCILLATIONS AND WAVES of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS OSCILLATIONS AND WAVES
- Additional Exercises
- Advanced Problems For Competitions
- Assertion-Reason Type Questions
- conceptual problems
- CURIOSITY QUESTION
- Fill In The Blanks
- Higher Order Thinking Skills
- integer type question
- JEE mains adv..(multiple choice quection)
- Long Answer Questions
- Multiple Choice Question
- Multiple Choice Question-I
- Multiple Choice Question-II
- multiple choice Questions
- NCERT CHAPTER
- NCERT EXERCISES WITH SOLUTIONS
- PROBLEMS FOR PRACTICE
- SAMPLE PROBLEM
- Short Answer Questions
- SOLVED EXAMPLES
- Value Based Questions
- Very Short Answer Questions
