Value (s) of 'a' for which ax2+(a−3)x+1<0 for at least one positive x.Solution in Bengali
Let f(x)=ax2+(a−3)x+1
Case (i)
If a>0, then f(x) will be negative only for those values of x which lie between the roots.
Since f(0)=1>0, the favourable graph according to the questions is shown in the following figure.
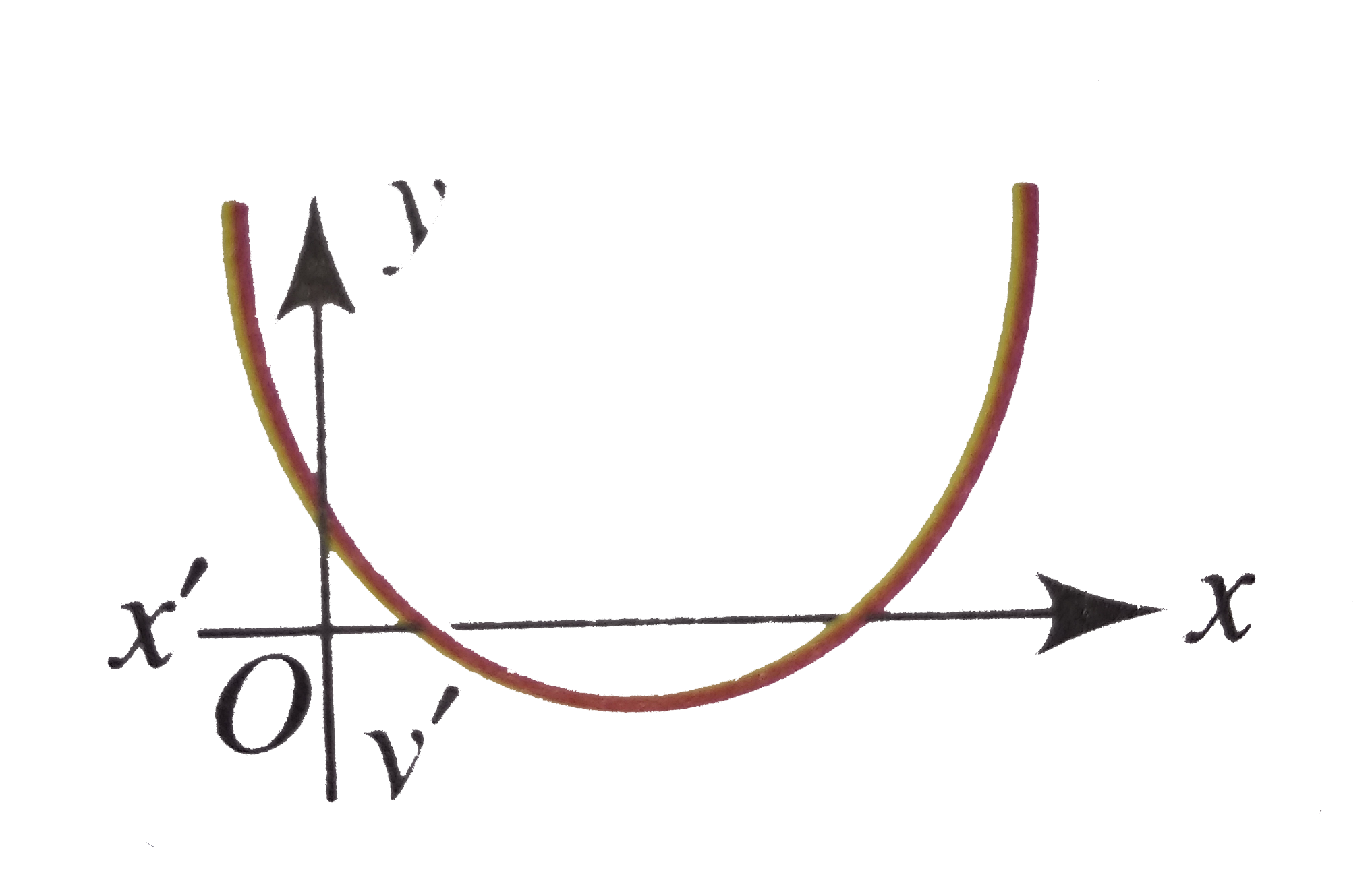
From the graph, we can see that both the roots are positive.
For this
(i) D>0⇒(a−3)2−4a>0
⇒a<1ora>9 (i)
(ii) Sum >0 and product >0
⇒−(a−3)>0and1/a>0
⇒a<3 (ii)
From (i) and (ii), a<1
But a>0⇒a∈(0,1)
Case (ii) : a<0
Since f(0)=1>0, the graph is as shown in the following figure :
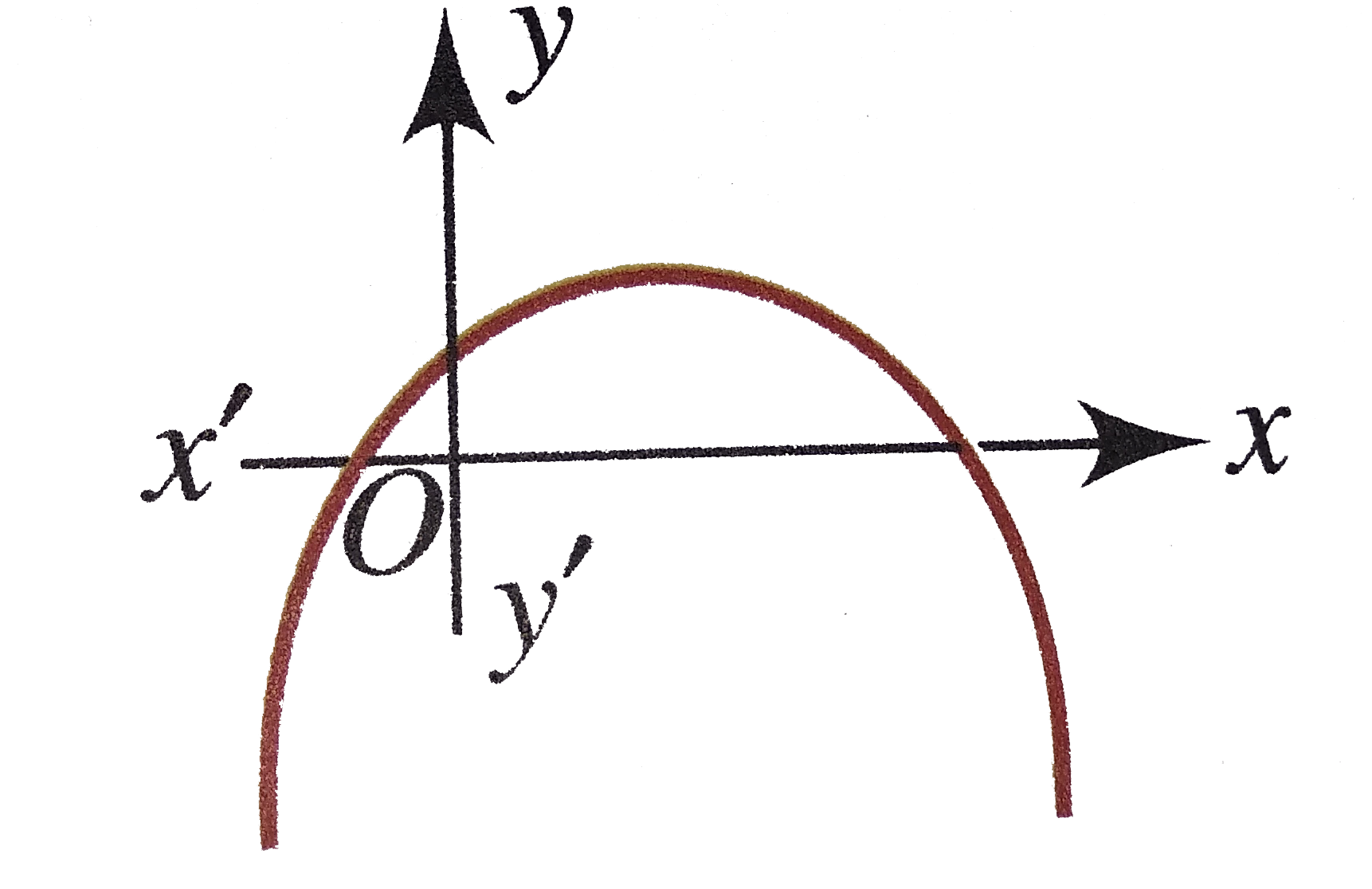
From the graph ax2+a(a−3)x+1<0, for at least one positive x.
Case (iii): a=0
If a=0,f(x)=−3x+1
⇒ f(x)<0,∀x>1/3
Thus, from all the cases, the required set of values of 'a' is (−∞,1).
Related Playlists
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
04:30View SolutionDraw the graph of y=(x−1)(x2−x+1).
06:12View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
02:22View SolutionThe set of exhaustive values of a for which the equation |ax-2|=2x^(2)+ax+4 has at least one positive root,is
01:44View SolutionLeast integral value of (s) of a for which 4^(x)-(a-2)*2^(x)+a<0 for at least one x in (0,oo) is (are)
01:44View SolutionConditions on a and b for which x^(2)-ax-b^(2) is less than zero for at least one positive x are
12:21View SolutionFind the least positive value of x such that
78+x=3(mod 5)02:50View SolutionFind the least positive value of x such that
89=(x+3)(mod 4)04:39View SolutionThe value of 'a' for which the quadratic expression ax^(2)+|2a-3|x-6 is positive for exactly two integral values of x is
06:29View SolutionFind the least positive value of x such that 197≡(x+3) (mod 5).
05:18View SolutionThe least integral value of a such that √9−a2+2ax−x2>√16−x2 for at least one positive x
03:31View SolutionThe least positive integral value of λ for which f(x)=3x32+λx23+x+7 has a point of maxima
01:56View Solutiona तथा b के शर्ते ज्ञात कीजिये जिसके लिए x2−ax−b2<0 कम से कम एक धनात्मक x के लिए
08:58View SolutionFind the value of a for which ax2+(a−3)x+1<0 for at least one positive real x.
05:07View Solutionx2+1<0
06:53View SolutionFind the value(s) of 'a' for which the inequality tan2x+(a+1)tanx−(a−3)<0, is true for at least one x∈(0,π2).
View Solution

