Using vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
Video Solution
Text Solution
Let ABCD and ABFE are parallelograms on the same base AB and between the same parallel lines AB and DF.
Here, AB||CD and AE||BF
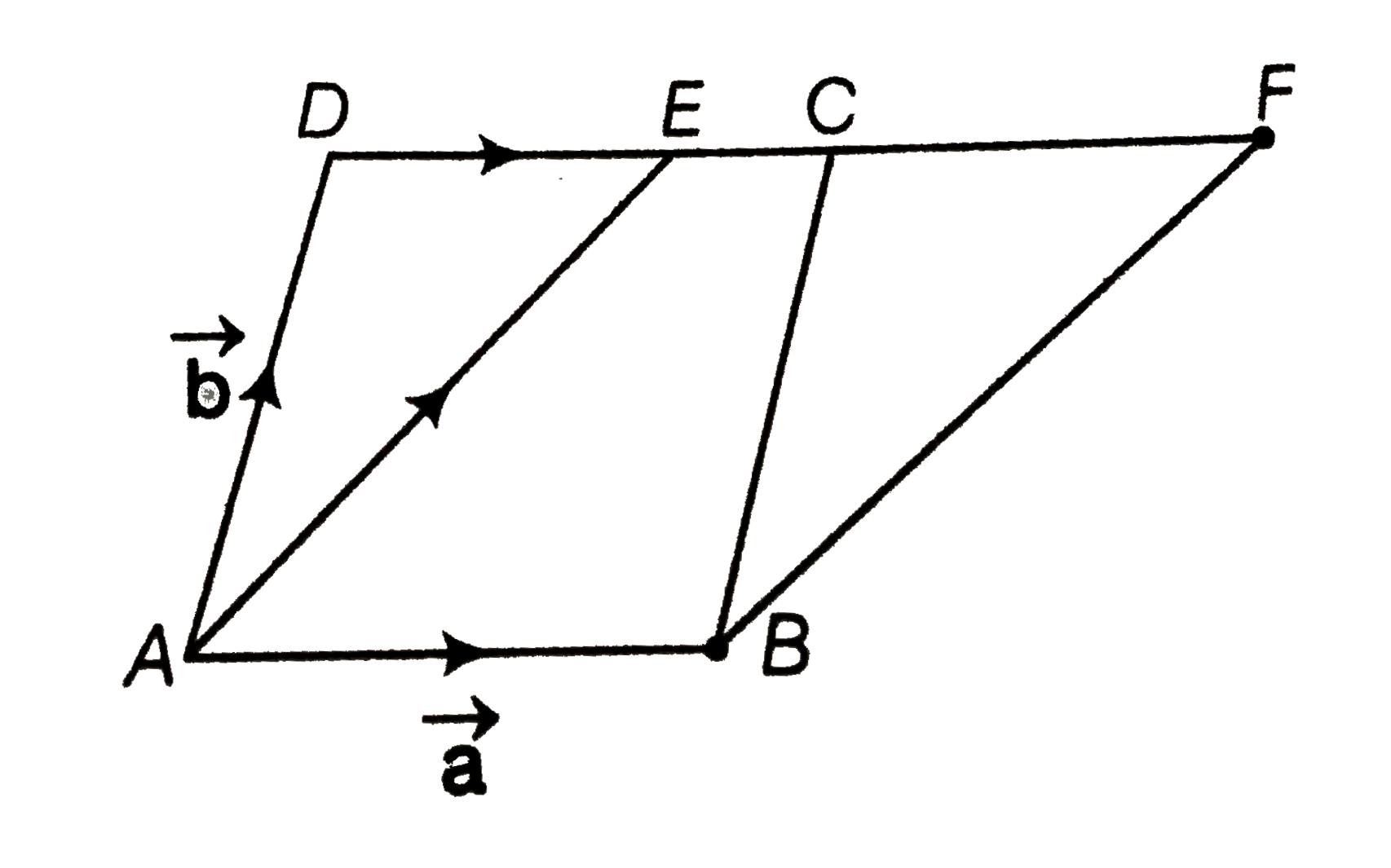
Let −−→AB=→aand−−→AD=→b :. Area of parallelogram ABCD=→a×→b
Now, area of parallelogram ABFE=−−→AB×−−→AE
=−−→AB×(−−→AD+−−→DE)
=−−→AB×(→b+k→a) [let−−→DE=k→a,where k is a scalar]
=→a×(→a+k→a)
=(→a×→b)+(→a×k→a)
=(→a×→b)+k(→a+→a)
=(→a×→b) [∴→a×→a=0]
= Area of parallelogram ABCD
Hence proved.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Two parallelograms are on equal bases and between the same parallels.
The ratio of their areas isA1:2B1:1C2:1D3:1
Figures on the same base and between the same parallels
View SolutionProve by vector method that the parallelogram on the same base and between the same parallels are equal in area.
View SolutionTheorem 9.1 : Parallelograms on the same base and between the same parallels are equal in area.
View SolutionProve that parallelograms on the same base and between the same parallels have the same area.
View SolutionA ||gm and a rectangle on the same base and between the same parallels are equal in area
View SolutionThe area of parallelogram on the same base and between the same parallel lines are ………………..
View SolutionProve that If a triangle and a parallelogram are on the same base and between the same parallels, the area of the triangle is equal to half of the parallelogram.
View Solution
