The given figure shows a rectangle ABDC and a parallelogram ABEF, drawn on opposite sides of AB. Prove that :
(i) quadrilateral CDEF is a parallelogram, (ii) Area of quad. CDEF
= Area of rec. ABDC
+Area of//gm.ABEF.
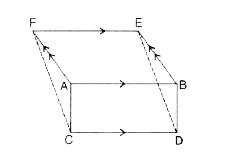
Step by step video & image solution for The given figure shows a rectangle ABDC and a parallelogram ABEF, drawn on opposite sides of AB. Prove that : (i) quadrilateral CDEF is a parallelogram, <be> (ii) Area of quad. CDEF = Area of rec. ABDC + "Area of" ////gm.ABEF. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)16videos
AREA THEOREMS
- BOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )22videos
AREA THEOREMS
- BOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )22videos
AREA THEOREMS
- BOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)12videos
AREA AND PERIMETER OF PLANE FIGURES
- BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA12videos
CHAPTER REVISION (STAGE 2)
Similar Questions
The along side figure shows a parallelogram ABCD in which AE = EF = FC.
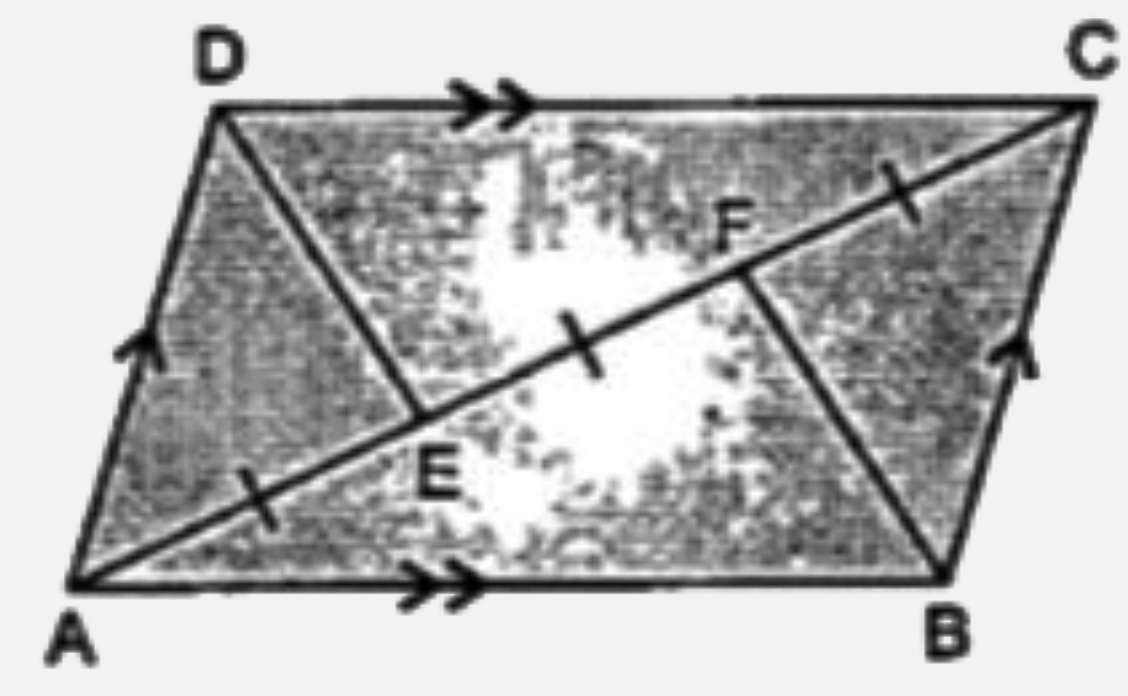
Prove that :
(i) DE is parallel to FB
(ii) DE = FB
(iii) DEBF is a parallelogramView SolutionIn the given figure, ABCD and ABEF are parallelograms. If O is the mid-point of BC, show that : DC = CF = FE.
 View Solution
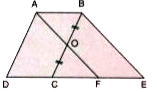
View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED
 View Solution
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) □BDEF=12× area of ΔABC
 View Solution
View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
area(ΔABX)=area( .ACXD)
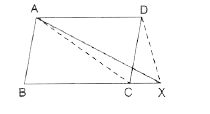 View Solution
View SolutionThe given figure shows a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD of the parallelogram ABCD. Prove that :
(i) ∠SAQ=∠ABC
(ii) SQ = AC
 View Solution
View SolutionOne side of a parallelogram is 20cm and its distance from the opposite side is 16cm. Find the area of the parallelogram.
View SolutionThe given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
[Join B and R]
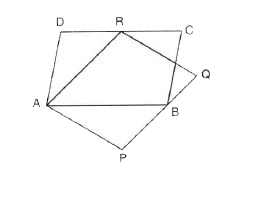 View Solution
View SolutionThe given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
[Join B and R]
 View Solution
View SolutionIn parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX=YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.View Solution
