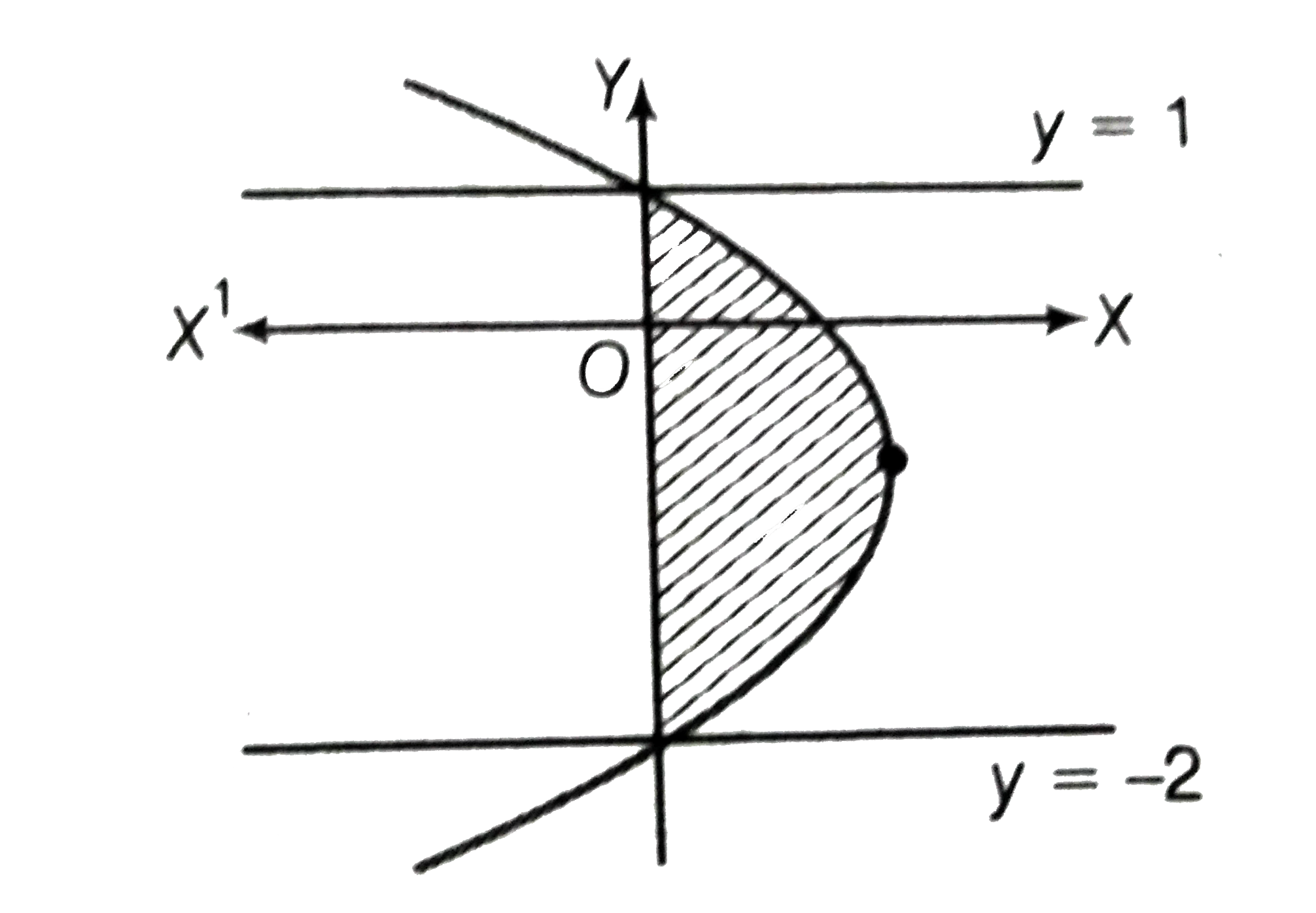
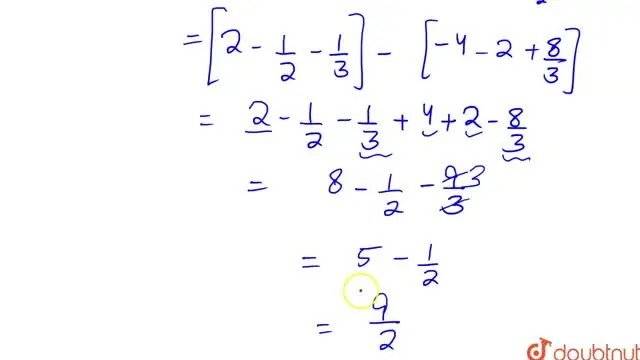The area bounded by the curve x=2−y−y2 and Y-axis is
A
32 sq units
B
52 sq units
C
92 sq units
D
None of these
Video Solution
Text Solution
The correct Answer is:C
For the intersection point of the curve and Y-axis, put x = 0
∴2−y−y2=0
⇒y+y2=2
⇒y=1,−2
The required area =∫1−2xdy
=∫1−2(2−y−y2)dy=[2y−y22−y33]1−2
(2−12−13)−(−4−42+83)=6+32−3=92 sq units
|
Updated on:21/07/2023
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - Exercise 234videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner6videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER21videos
APPLICATIONS OF DERIVATIVES
Similar Questions
The area bounded by the curve x=6y−y2 and the y-axis is
View SolutionThe area bounded by the curve x=4−y2 and the Y-axis is
View SolutionThe area bounded by the curve y=x(x2−1) and x-axis is
View SolutionArea bounded by the curve y=x2+x−6 and the X-axis is
View Solutionthe area included between the curve xy2=a2(a−x) and y -axis is -
View SolutionThe area bounded by the curves y=2−|2−x| and |x|y=3 is
View SolutionThe area bounded by the curve y2=4ax, Y-axis between y=-a and y= a is
View SolutionThe area bounded by the curve |x|+|y|=1 and axis of x, is given by
View SolutionThe area of the region bounded by the curves x=y2−2 and x=y is
View SolutionThe area bounded by the curves y2=x3and|y|=2x.
View Solution