Statement-1: If f(x)=∫x1loget1+t+t2dt, then
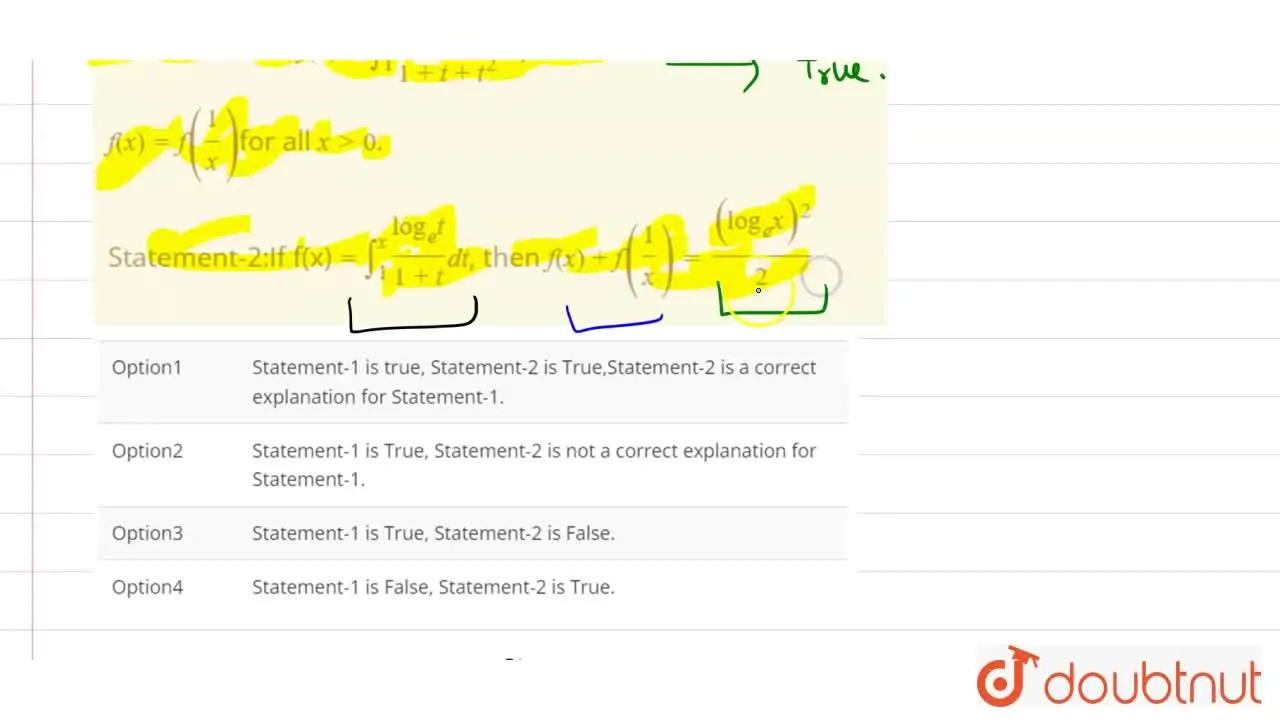
f(x)=f(1x)for all x>0.
Statement-2:If f(x)=∫x1loget1+tdt, then f(x)+f(1x)=(logex)22
Statement-1 is true, Statement-2 is True,Statement-2 is a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is not a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is False.
Statement-1 is False, Statement-2 is True.
The correct Answer is:B
If f(x)=x∫1loget1+t+t2dt, then
f(1x)=1/x∫1loget1+t+t2dt
⇒f(1x)=x∫1logeu1+u+u2du, where t=1u
⇒f(1x)=f(x)
So, statement-1 is true.
If f(x)=x∫1loget2+tdt, then
(1x)=1/x∫1loget1+tdt
⇒f(1x)=x∫1logeuu(1+u)du, where t=1u
⇒f(1x)=x∫1loget(l+t)dt
∴f(x)+f(1x)=x∫1logett+1(1+1t)dt
=x∫1logttdt=[(loget)22]x1=(logex)22
So, statement-2 is also true.
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Exercise147videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 160videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section I - Solved Mcqs145videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise86videos
CONTINUITY AND DIFFERENTIABILITY
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
Similar Questions
Statement-1: If f(x)=∫x1loget1+t+t2dt, then
f(x)=f(1x)for all x>0.
Statement-2:If f(x)=∫x1loget1+tdt, then f(x)+f(1x)=(logex)22View SolutionIf f(x)=∫x1logt1+tdtthenf(x)+f(1x) is equal to
View SolutionIf F(x)=∫x1lnt1+t+t2dt then F(x)=−F(1x).
View SolutionIf f(x)=∫x1lnt1+tdt, then
View SolutionIff(x)=∫x1logt1+t+t2dx∀x≤1,thenprovethatf(x)f(1x).
View SolutionIf f(x)=∫x1(logt)(1+t+t2)dt∀x≥1, then prove that f(x)=f(1x).
View SolutionIf f(x)=∫x21x2cos√tdt, then f'(1)=
View SolutionIf f(x)=1+x+∫x1(ln2t+2lnt)dt then f(x) increases in
View SolutionFor x>0, let f(x)=∫x1loget1+tdt find the function f(x)+f(1x) and show that f(e)+f(1e)=12
View SolutionIf f(x)=∫xlogexdtx+t then f'(x)=
View Solution