$\int_{0}^{10} | x (x - 1) (x - 2) | d x$ is equal to

A

$160.05$

B

$1600.5$

C

$16.005$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let $f (x) = (x - 1) (x - 2)$ . The signs of f(x) for differenta values of x are as shown belown

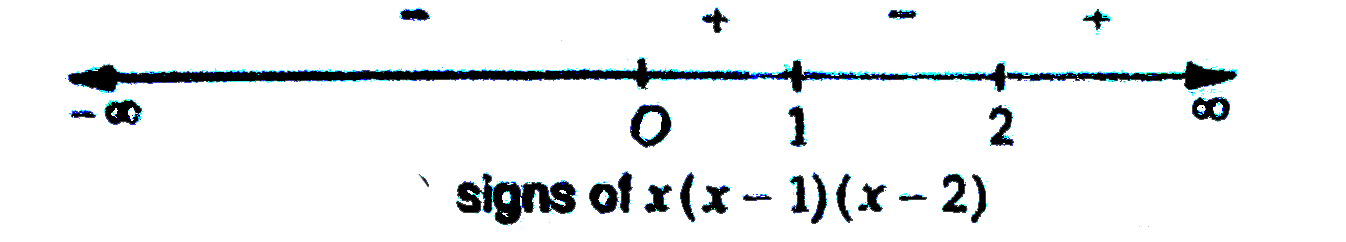
$\begin{matrix} - x (x - 1) (x - 2) = (- x^{3} - 3 x^{2} + 2 x), & if x < 0 x (x - 1) (x - 2) = x^{3} - 3 x^{2} + 2 x, & if 0 \leq x < 1 - x (x - 1) (x - 2) = - (x^{3} - 3 x^{2} + 2 x), & if 1 \leq x < 2 x (x - 1) (x - 2) = x^{3} - 3 x^{2} + 2 x, & if x > 2 \end{matrix}$
$∴ 10 \int 0 | x (x - 1) (x - 2) | d x$
$\Rightarrow I = 1 \int 0 | x (x - 1) (x - 2) | d x + 2 \int 1 | x (x - 1) (x - 2) | d x$
$\Rightarrow I = 1 \int 0 (x^{3} - 3 x^{2} + 2 x) d x + 2 \int 1 - (x^{3} - 3 x^{2} + 2 x) d x + 10 \int 2 (x^{3} - 3 x^{2} + 2 x) d x$
$\Rightarrow I = {[\frac{x^{4}}{4} - x^{3} + x^{2}]}_{0}^{3} - {[\frac{x^{4}}{4} - x^{3} + x^{2}]}_{1}^{3} + {[\frac{x^{4}}{4} - x^{3} + x^{2}]}_{2}^{3}$
$\Rightarrow I = \frac{1}{2} + 1600 = 1600.5$

|

Updated on:21/07/2023

Class 12 MATHS DEFINITE INTEGRAL

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$\int_{0}^{5} \frac{1}{(x - 1) (x - 2)} d x$ is equal to
A $log . \frac{27}{32}$
B $log . \frac{32}{27}$
C $log . \frac{8}{9}$
D $log . \frac{3}{4}$
Question 2 - Select One
The value of $\int_{0}^{1} x^{2} e^{x} d x$ is equal to
A $e - 2$
B $e + 2$
C $e^{2} - 2$
D $e^{2}$
Question 3 - Select One
If {x} denotes the fractional part of x, then $\int_{0}^{x} ({x} - \frac{1}{2}) d x$ is equal to
A $\frac{1}{2} {x} ({x} + 1)$
B $\frac{1}{2} {x} ({x} - 1)$
C ${x} ({x} - 1)$
D ${x} ({x} + 1)$

OBJECTIVE RD SHARMA-DEFINITE INTEGRALS-Section I - Solved Mcqs

Home
Ask Doubt
Profile