Show that, in a parallelogram ABCD, the internal and external bisectors of ∠Aand∠B from a rectangle.
Step by step video, text & image solution for Show that, in a parallelogram ABCD, the internal and external bisectors of angleA and angleB from a rectangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Revision Exercise (short Answer Questions )
Explore 10 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
Knowledge Check
The measure of the angle between the internal and external bisectors of an angle is
A60∘B70∘C80∘D90∘In a parallelogram ABCD, M is the midpoint of BD and BM is bisector of ∠B. The measure of ∠AMB is.
A45∘B60∘C90∘D120∘In a parallelogram ABCD, the bisector of anl≥A also bisects BC at E, find the AD.
AABB2ABC3ABD12AB
Show that the bisectors of angles of a parallelogram form a rectangle.
View SolutionIn a parallelogram ABCD∠B=110∘ determine the measure of ∠A and ∠D.
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
View SolutionIn the adjoining figure, ABCD is a parallelogram , AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=90∘.
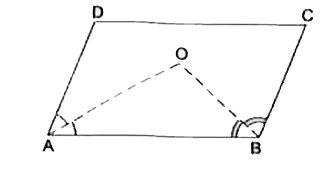
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View Solution

