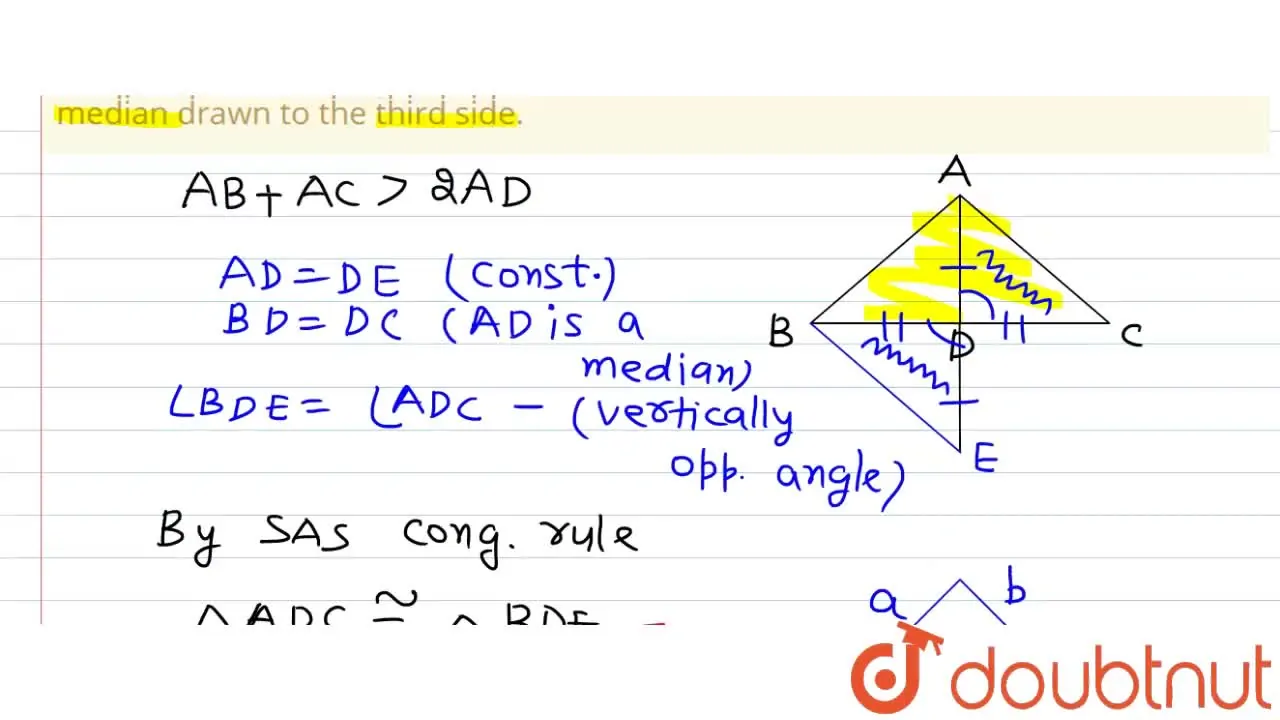
Prove that any two sides of a triangle are together greater than twice the median drawn to the third side.
Step by step video & image solution for Prove that any two sides of a triangle are together greater than twice the median drawn to the third side. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
View SolutionWhich of the following statements are true (T) and which are false (F)?
(i) Sum of the three sides of a triangle is less than the sum of its three altitudes.
(ii) Sum of any two sides of a triangle is greater than twice the median drawn to the third side.
(iii) Sum of any two sides of a triangle is greater than the third side.
(iv) Difference of any two sides of a triangle is equal to the third side.
(v) If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
(vi) Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.View SolutionProve that the perimeter of a triangle is greater than the sum of its three medians.
View SolutionTheorem 6.2 : If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
View SolutionIf two sides of a triangle are ˆi+2ˆjandˆi+ˆk, then find the length of the third side.
View SolutionIf two side of a triangle are ˆi+2ˆjandˆi+ˆk , then find the length of the third side.
View SolutionTheorem 7.8 : The sum of any two sides of a triangle is greater than the third side.
View SolutionTwo sides of a triangle are 4 cm and 10 cm. what is the possible range of length of the third side ?
View SolutionProve that the sum of the sides of a quadrilateral is greater than twice of one of its diagonal.
View SolutionTwo sides of a triangle are 15cm and 20cm. The perimeter of the triangle is 50cm. What is the third side?
View Solution