OPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16Solution in Bengali
Step by step video & image solution for O P Q R is a square and M ,N are the midpoints of the sides P Q and Q R , respectively. If the ratio of the area of the square to that of triangle O M N is lambda:6, then lambda/4 is equal to 2 (b) 4 (c) 2 (d) 16 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions877videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type11videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
Similar Questions
The equation esinx−e−sinx−4=0 has
03:01View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to03:43View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
 01:31View Solution
01:31View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
 02:05View Solution
02:05View SolutionOPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
03:14View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
02:40View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
01:38View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
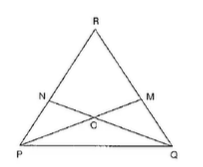 05:43View Solution
05:43View SolutionOPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is (a) 8:1 (b) 2:1 (c) 8:3 (d) 7:3
03:18View SolutionOPQR is a square and M,N are the midpoints of the sides PQ and QR , respectively. If the ratio of the area of the square to that of triangle OMN is λ:6, then λ4 is equal to 2 (b) 4 (c) 2 (d) 16
04:12View SolutionOPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
03:10View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
02:39View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
03:09View SolutionIn △PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MN∣∣QR .
04:51View SolutionIn triangle PQR, if PQ=RQ and L, M and N are the mid-points of the sides PQ, QR and RP respectively. Prove that LN=MN.
01:11View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
07:33View Solution


