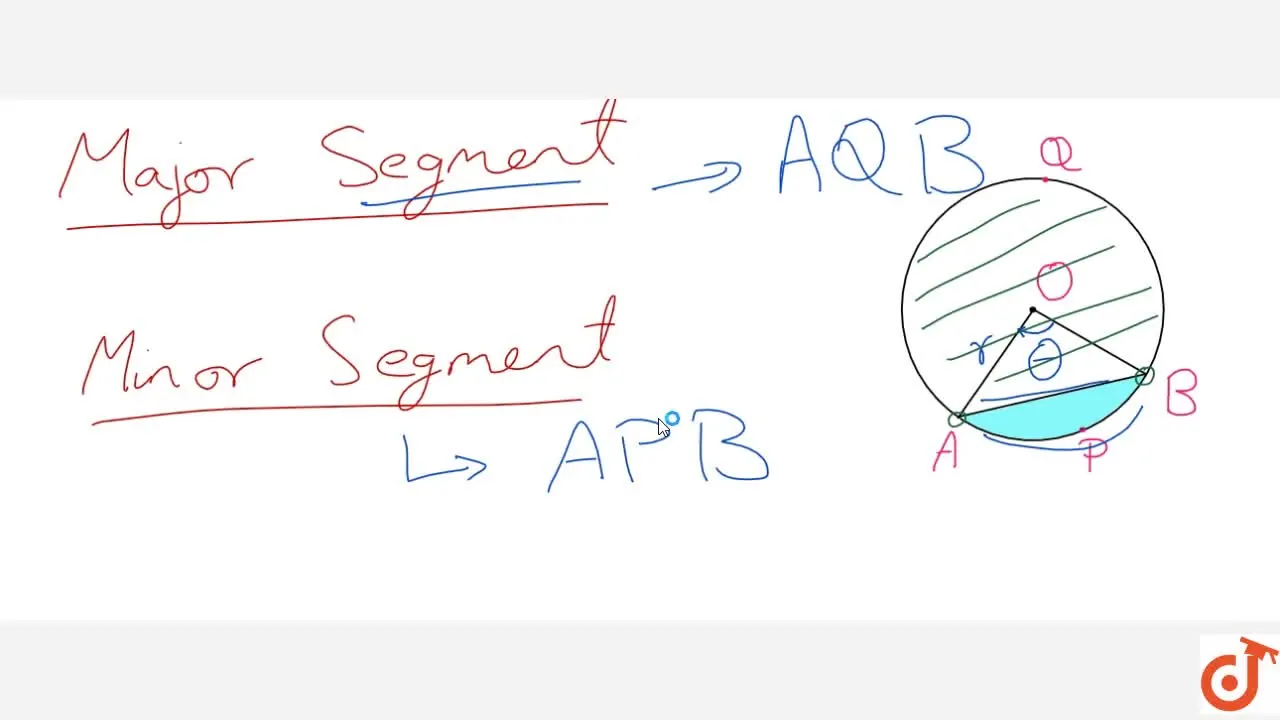
Major and Minor segment
Step by step video & image solution for Major and Minor segment by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
Major and Minor Arc
View SolutionA chord PQ of a circle of radius 10 cm makes an angle of 60∘ at the centre of the circle. Find the area of the major and the minor segment
View SolutionA chord of a circle of radius 15 cm subtends an angle of 60∘ at the centre . Find the areas of the corresponding minor and major segments of the circle.
View SolutionA chord of a circle of radius 14 cm makes a right angle at the centre. Find the areas of the minor and major segments of the circle.
View SolutionMajor and minor grooves occurs in
View SolutionAngle formed in minor segment of a circle is
View SolutionThe radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
View SolutionA chord PQ of a circle4 with radius 15 cm subtends an angle of 60∘ with the centre of the circle.
Find the area of the inor as well as the major segement. (π=3.14,√3=1.73)
Given: r=15cm, θ=60∘
To find A(minor segment)
A(major segment)View SolutionA chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the minor and major segments. [Take π=314 and √3=1.732]
View SolutionA chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding :
Minor segmentView Solution