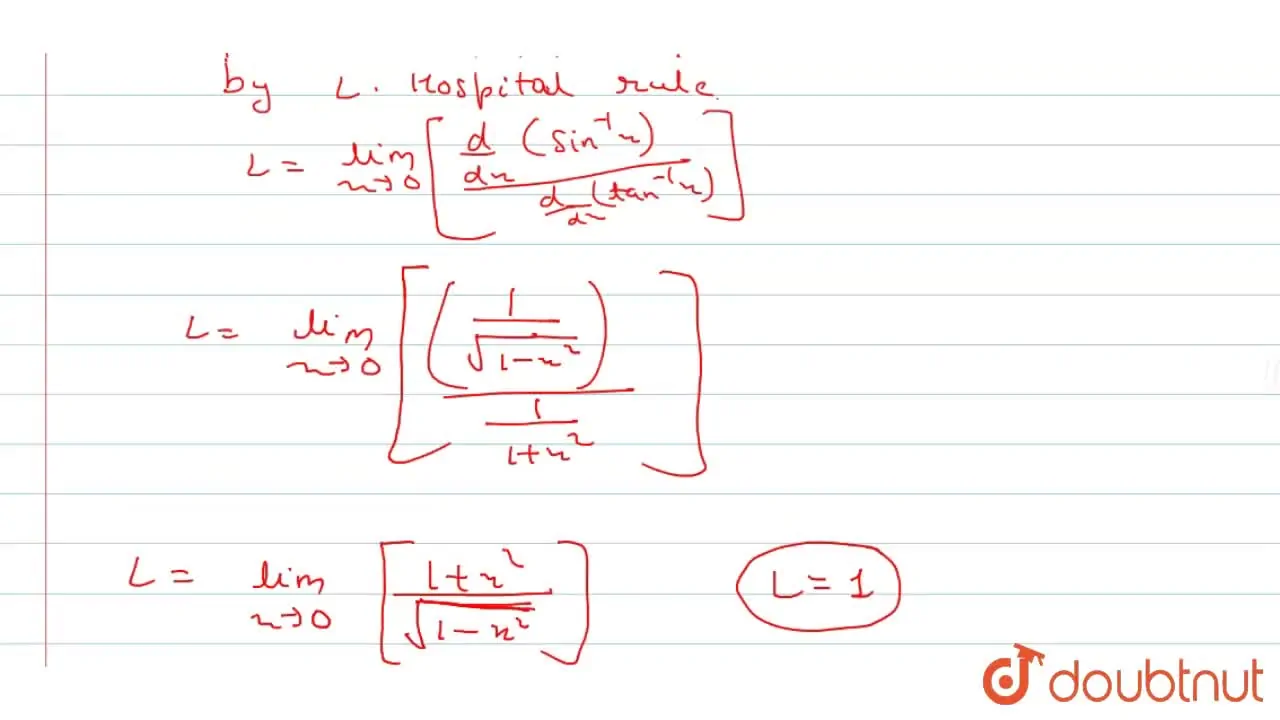
limx→0[sin−1xtan−1x]= (where [.] denotes the greatest integer function)
0
1
−1
none of these
The correct Answer is:B

L=limx→0[sin−1xtan−1x]
=limx→0⎡⎢⎣sin−1xxtan−1xx⎤⎥⎦
=[1(but gt 1)1(but lt 1)]
=1
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - ComprehensionType2videos
LIMITS
- BOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Multiple Correct Answer Type2videos
LIMITS
- BOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Archives JEE ADVANCED2videos
LIMITS
- BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
- BOOK - CENGAGE ENGLISHCHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.210videos
LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
Similar Questions
limx→−131x[−1x]= (where [.] denotes the greatest integer function)
View Solutionlimx→0[min(y2−4y+11)sinxx] (where [.] denotes the greatest integer function) is
View Solutionf(x)=[tan−1x] where [.] denotes the greatest integer function, is discontinous at
View SolutionThe value of limx→π2[x3]ln(sinx) (where, [.] denotes the greatest integer function)
View Solutionlimx→0[sin(sgn(x))(sgn(x))], where [.] denotes the greatest integer function, is equal to
View SolutionIf f(x)=[sin−1(sin2x)] (where, [] denotes the greatest integer function ), then
View Solutionlimx→0[−2xtanx], where [.] denotes greatest integer function is
View SolutionProve that [limx→0sinx.tanxx2]=1,where [.] represents greatest integer function.
View SolutionSolve (i) limx→∞tan−1x
(ii) limx→−∞tan−1x
(where [.] denotes greatest integer function)View Solutionf(x)=cosec−1[1+sin2x], where [⋅] denotes the greatest integer function.
View Solution