Let f(x) be defined for all x∈R such that limx→0[f(x)+log(1−1ef(x))−log(f(x))]=0. Then f(0) is
0
1
2
3
The correct Answer is:A
To solve the problem, we need to analyze the limit given in the question:
limx→0(f(x)+log(1−1ef(x))−log(f(x)))=0
Step 1: Rewrite the limit expression
We can rewrite the logarithmic terms using the property of logarithms:
log(1−1ef(x))−log(f(x))=log⎛⎜⎝1−1ef(x)f(x)⎞⎟⎠
Thus, the limit can be expressed as:
limx→0⎛⎜⎝f(x)+log⎛⎜⎝1−1ef(x)f(x)⎞⎟⎠⎞⎟⎠=0
Step 2: Analyze the limit as x→0
As x→0, we need to consider the behavior of f(x). Let's denote f(0)=L. The limit becomes:
limx→0⎛⎜⎝f(x)+log⎛⎜⎝1−1ef(x)f(x)⎞⎟⎠⎞⎟⎠=0
Step 3: Substitute f(0) into the limit
If we assume that f(0)=L, we can substitute f(x) with L in the limit:
L+log⎛⎜⎝1−1eLL⎞⎟⎠=0
Step 4: Solve for L
Rearranging gives us:
log⎛⎜⎝1−1eLL⎞⎟⎠=−L
Exponentiating both sides gives:
1−1eLL=e−L
This can be rewritten as:
1−1eL=Le−L
Step 5: Analyze the equation
Rearranging gives us:
1=Le−L+1eL
Step 6: Consider the case L=0
If we assume L=0:
1=0⋅e0+1e0=1
This holds true, suggesting that f(0)=0 is a valid solution.
Conclusion
Thus, we conclude that:
f(0)=0
We can rewrite the logarithmic terms using the property of logarithms:
As x→0, we need to consider the behavior of f(x). Let's denote f(0)=L. The limit becomes:
If we assume that f(0)=L, we can substitute f(x) with L in the limit:
Rearranging gives us:
Rearranging gives us:
If we assume L=0:
Thus, we conclude that:
Topper's Solved these Questions
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - ComprehensionType
2 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Multiple Correct Answer Type
2 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Archives JEE ADVANCED
2 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGE ENGLISHCHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
limx→0[1x−log(1+x)x2]=
View Solutionlimx→0[1x−log(1+x)x2]=
View SolutionEvaluate limx→0f(x), where
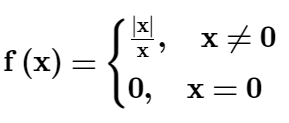
View Solutionlimx→0(log(1+x)x)
a) 1
b) e
a) -1
b) -e
View SolutionLet p(x) be a function defined on R such that limx→∞f(3x)f(x)=1,p'(x)=p'(1−x),for allx∈[0,1],p(0)=1andp(1)=41.Then,∫10p(x)dx equals
View SolutionIf f(x)=|x|x, then show that limx→0f(x) does not exist.
View SolutionThe value of limx→0loge(1+x)−xx{(1+x)1/x−e} equal to
View SolutionLet f(x) be defined for all x>0 and be continuous. Let f(x) satisfies f(xy)=f(x)−f(y) for all x,yandf(e)=1. Then (a) f(x) is unbounded (b) f(1x)→0 as x→0 (c) f(x) is bounded (d) f(x)=(log)ex
View SolutionLet f(X) be a polynomila of degree four having extreme values at x =1 and x=2.If limx→0[1+f(x)x2]=3 then f(2) is equal to
View SolutionIf f(x)=log|x|,x≠0 then f'(x) equals
View Solution
