Let →aand→b are two vectors inclined at an angle of 60∘,If|→a|=∣∣→b∣∣=2 ,the the angle between →aand→a+→b is
30∘
60∘
45∘
none of these
The correct Answer is:A
we have,
|→a|=∣∣→b∣∣=2and→a.Vecb=|→a|∣∣→b∣∣cos60∘=2
Now,
∣∣→a+→b∣∣2=|→a|2+∣∣→b∣∣2+2(→a.→b)
⇒∣∣→a+→b∣∣2=4+4+4
⇒∣∣→a+→b∣∣=2√3
Let θ the angle between →aand→a+→b1 . then .
cosθ=→a.(→a+→b)|→a|∣∣→a+→b∣∣=→a.→a+→a.→b|→a|∣∣→a+→b∣∣=4+22×2√3=√32
⇒θ=30∘
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALER AND VECTOR PRODUCTS OF TWO VECTORS EXERCISE - Section I - Solved Mcqs12videos
SCALER AND VECTOR PRODUCTS OF TWO VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise65videos
SCALAR AND VECTOR PRODUCTS OF THREE VECTORS
- BOOK - OBJECTIVE RD SHARMACHAPTER - SOLUTIONS OF TRIANGLES EXERCISE - Exercise20videos
SOLUTIONS OF TRIANGLES
Similar Questions
If ∣∣→a.→b∣∣=∣∣→a×→b∣∣ , then the angle between →aand→b is
View SolutionLet →a and →b are unit vectors inclined at an angle α to each other , if ∣∣→a+→b∣∣<1 then
View SolutionIf ∣∣→a−→b∣∣=|→a|=∣∣→b∣∣=1 , then the angle between →aand→b , is
View SolutionIf ∣∣→A−→B∣∣=∣∣→A∣∣=∣∣→B∣∣, the angle between →A and →B is
View SolutionIf ∣∣→a+→b∣∣2=|→a|2+∣∣→b∣∣2 then angle between →a and →b is
View SolutionIf →a and →b are unit vectors inclined at an angle θ, then the value of ∣∣→a−→b∣∣ is
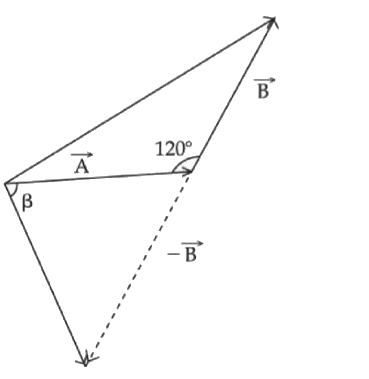
View SolutionThe angle between vector (→A) and (→A−→B) is :
 View Solution
View Solutionvectors →aand→b are inclined at an angle θ=60∘. If |→a|=1,∣∣→b∣∣=2, then [(→a+3→b)×(3→a−→b)]2 is equal to
View SolutionIf ∣∣→A+→B∣∣=∣∣→A∣∣+∣∣→B∣∣, then angle between →A and →B will be
View SolutionVectors →a and →b are inclined at an angle θ=120∘ . If |→a|=∣∣→b∣∣=2 , then [(→a+3→b)×(3→a+→b)]2 is equal to
View Solution


