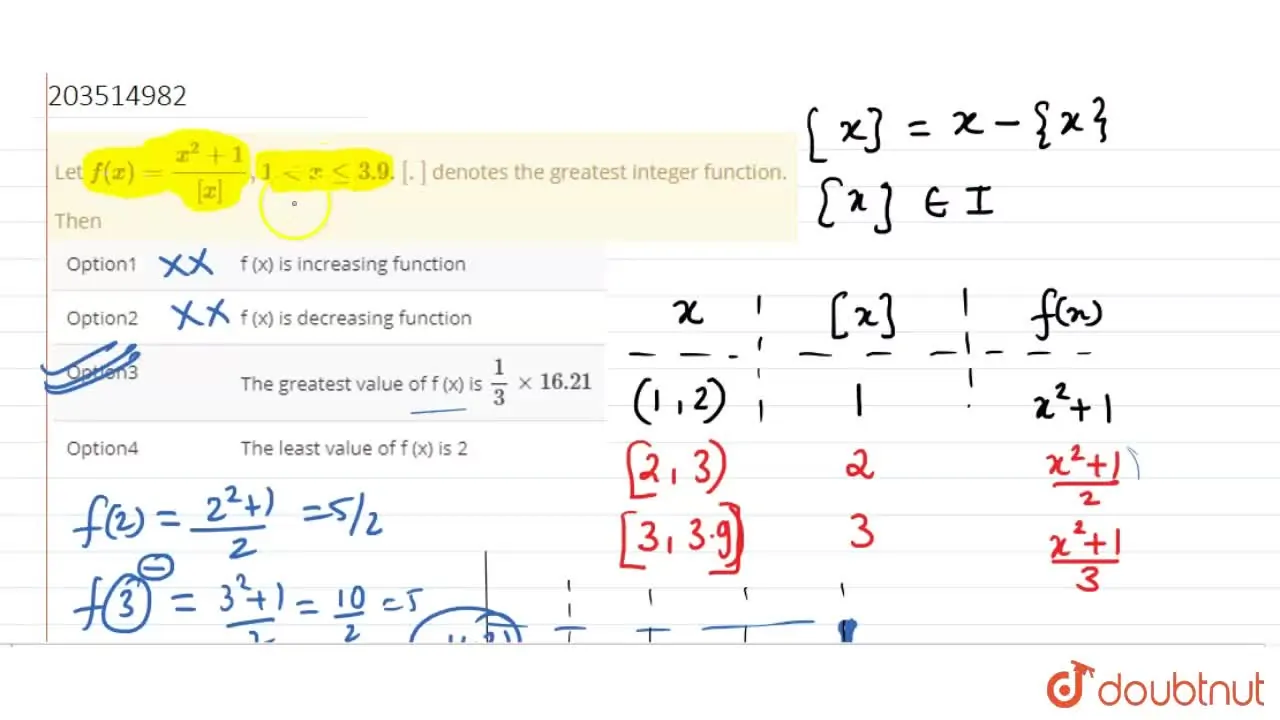
Let f(x)=x2+1[x],1<x≤3.9.[.] denotes the greatest integer function. Then
f (x) is increasing function
f (x) is decreasing function
The greatest value of f (x) is 13×16.21
The least value of f (x) is 2
The correct Answer is:C
Here, f(x)=x2+1,1<x<2
x2+12,2≤x<3, x2+13,3≤x≤3.9
f'(x)>0 in each of the intervales and so f(x) is increasing in each of the intervals
∴ 2<f(x)<5 in 1<x<2,52≤f(x)<5 in 2≤x<3,103≤f(x)≤13×16.21 in 3≤x≤3.9
Hence, the greatest value is 13×16.21
Similar Questions
Let f(x)=x2+2[x],1≤x≤3, where [.] is the greatest integer function. Then the least value of f(x) is
View SolutionLet f(x) =[x]2+[x+1]−3, where [.] denotes the greatest integer function. Then
View SolutionLet [.] denote the greatest integer function and f(x)=[tan2x]. Then
View SolutionLet f(x)=sec−1[1+cos2x], where [.] denotes the greatest integer function. Then the
View SolutionFor a function f(x)=2(x2+1)[x] (where [.] denotes the greatest integer function), if 1≤x<4. Then
View SolutionLet f(x)=[x]cos(π[x+2]) where [ ] denotes the greatest integer function. Then, the domain of f is
View SolutionLet f(x)=(−1)[x] where [.] denotes the greatest integer function), then
View SolutionLet f(x)={1+|x|,x<−1[x],x≥−1 , where [.] denotes the greatest integer function. The find the value of f{f(−2,3)}.
View SolutionIf [.] denotes the greatest integer function, then f(x)=[x]+[x+12]
View SolutionLet f(x)=|x|andg(x)=[x], (where [.] denotes the greatest integer function) Then, (fog)'(−1) is
View Solution