Doubtnut Promotions Sticky

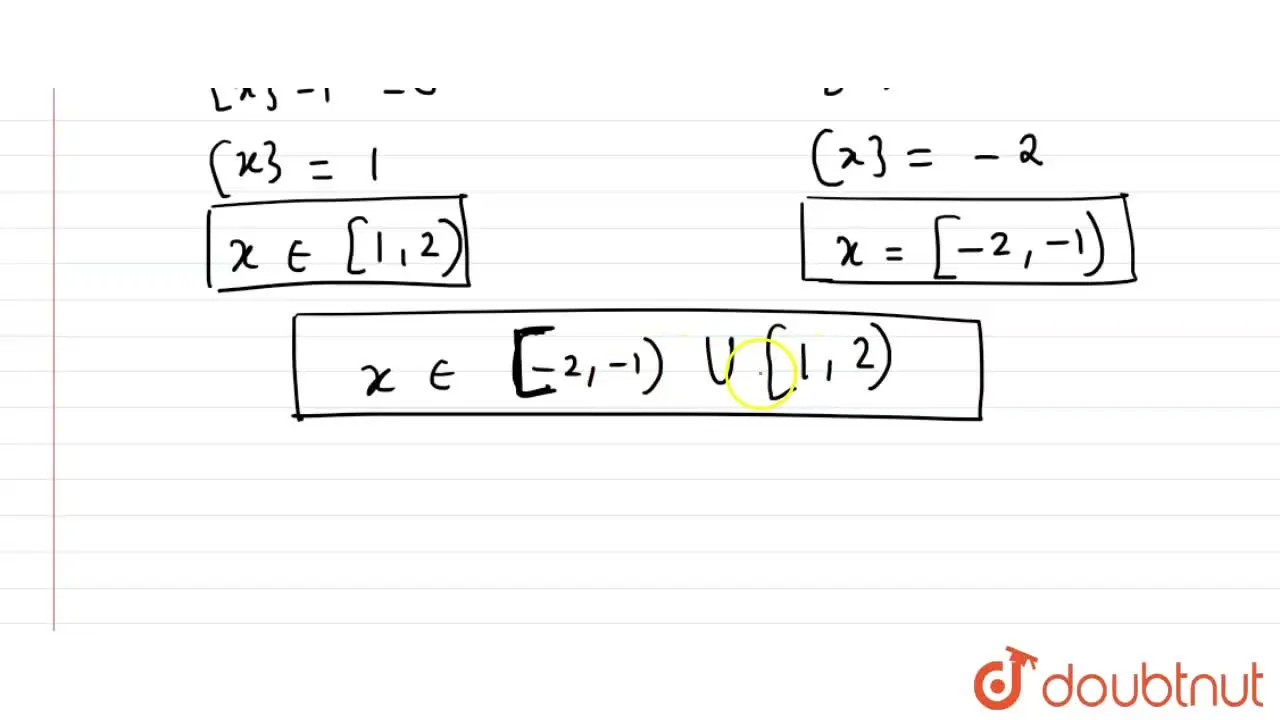
Let f(x) =[x]2+[x+1]−3, where [.] denotes the greatest integer function. Then

A

f(x)≠0 for all real values of x

B

f(x) = 0 for only two real value of x

C

f(x) = 0 for infinite values of x.

D

f(x) = 0 for no real value of x

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

|
Answer

Step by step video, text & image solution for Let f(x) = [x]^(2) + [x+1] - 3, where [.] denotes the greatest integer function. Then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSRELATIONS AND FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One or More

    Let f(x)=sec−1[1+cos2x], where [.] denotes the greatest integer function. Then the

    Adomain of f is R
    Bdomain of f is [1,2]
    Cdomain of f is [1,2]
    Drange of f is {sec−11,sec−12}
  • Question 2 - Select One

    Let f(x)=[x]cos(π[x+2]) where [ ] denotes the greatest integer function. Then, the domain of f is

    AxεR,x not an integer
    Bxε(−∞,−2)∪[−1,∞)
    CxεR,x≠−2
    Dxε(−∞,−1]
  • Question 3 - Select One

    Let f(x)=|x|andg(x)=[x], (where [.] denotes the greatest integer function) Then, (fog)'(−1) is

    A0
    Bdoes not exist
    C−1
    D1