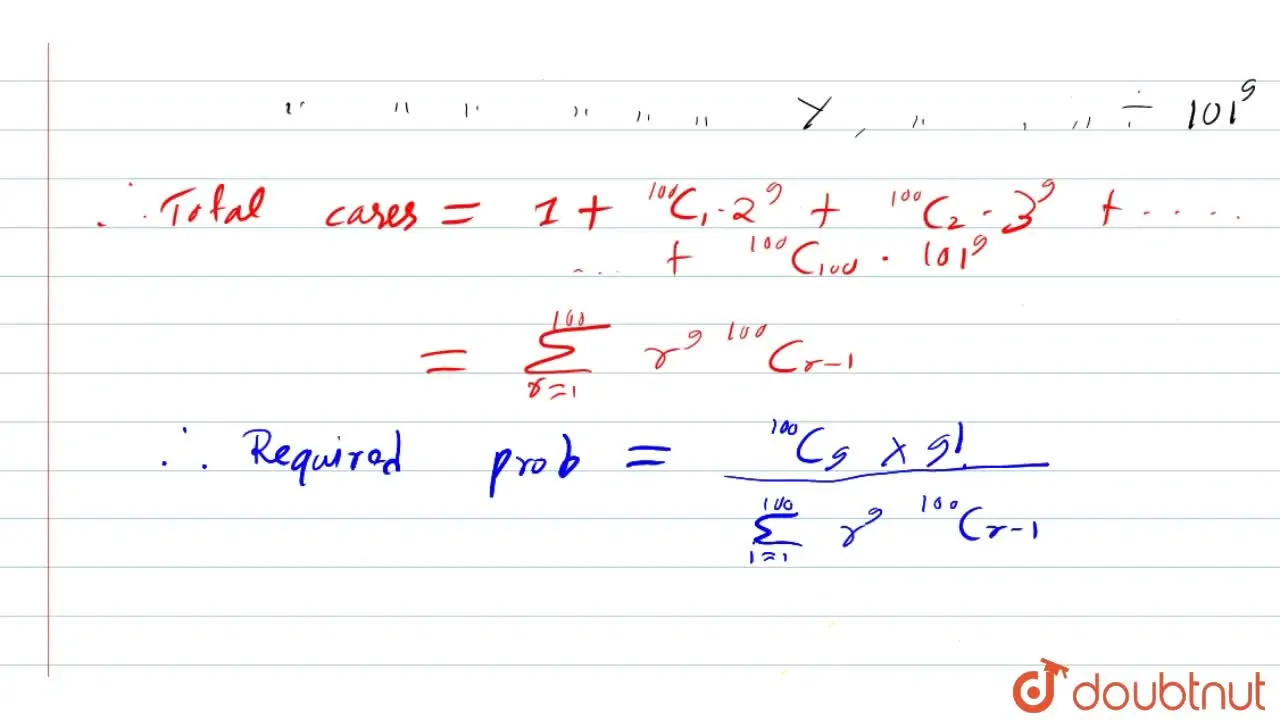Let a function f:X→Y is defined where X={0,1,2,3,….,9}, Y={0,1,2,…..,100} and f(5)=5, then the probability that the function of type f:X→B where B⊆Y is of bijective nature isSolution in Bengali
10!∑101r=1r9⋅100Cr−1
101C9⋅9!∑101r=1r10⋅100Cr
100C9⋅9!∑101r=1r10⋅101Cr
100C9⋅9!∑101r=1r9⋅100Cr−1
The correct Answer is:D
(d) Favourable cases for bijection is 100C9×9!
For total cases
'B' is set of one element, no. of function −1
'B' is set of two element, no. of function −29
'B' is set of three element, no. of function −39
.........
........
'B'=Y, No. of function =1019
∴ Total cases =1+100C1⋅29+100C2⋅39+....+100C100⋅1019
=101∑r=1r9⋅100Cr−1
∴ Required probability =100C9⋅9!∑101r=1r9⋅100Cr=1
Related Playlists
Similar Questions
Prove the following by using the principle of mathematical induction for all n∈N:13+23+33+...........+n3=(n(n+1)2)2
08:14View SolutionLet ω be a complex cube root unity with ω≠1. A fair die is thrown three times. If r1,r2andr3 are the numbers obtained on the die, then the probability that ωr1+ωr2+ωr3=0 is 1/18 b. 1/9 c. 2/9 d. 1/36
03:38View SolutionThe function f:N rarr N defined by f(x)=x-5[(x)/(5)] where N is a set of natural numbers,then
View SolutionLet y=f(x) and y=g(x) be two monotonic, bijective functions such that f(g(x) is defined than y=f(g(x)) is
02:04View SolutionLet a function f:X→Y is defined where X={0,1,2,3,….,9}, Y={0,1,2,…..,100} and f(5)=5, then the probability that the function of type f:x→B where B⊆Y is of bijective in nature is
06:53View SolutionLetf(3)=4andf'(3)=5. Then limx→3[f(x)] (where [.] denotes the greatest integer function) is
06:31View SolutionLet f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function.03:57View SolutionLet a function f:X→Y is defined where X={0,1,2,3,….,9}, Y={0,1,2,…..,100} and f(5)=5, then the probability that the function of type f:X→B where B⊆Y is of bijective nature is
04:43View SolutionLetf(3)=4andf'(3)=5. Then limx→3[f(x)] (where [.] denotes the greatest integer function) is
04:52View SolutionShow that the function f:R→R defined by f(x)=3x3+5 for all x∈R is a bijection.
View SolutionShow that the function f:R→R defined by f(x)=3x3+5 for all x∈R is a bijection.
05:04View SolutionIf X and Y are two nonzero sets where f:XtoY Function is defined while CsubeX for f(c)={f(x):x epsilonC} And DsubeY for f^(-1)(D)={x:f(x)epsilonD} anyone AsubeX And BsubeY Then for
02:36View SolutionShow that the function f:N→N defined by f(x)=2x+3, where x∈N, is not bijective.
04:37View SolutionLet f(x) = ([x]+1)/({x}+1) for f: [0, (5)/(2) ) to ((1)/(2) , 3] , where [*] represents the greatest integer function and {*} represents the fractional part of x. Draw the graph of y= f(x) . Prove that y=f(x) is bijective. Also find the range of the function.
08:26View SolutionLet a function f:X→Y is defined where X={0,1,2,3,….,9}, Y={0,1,2,…..,100} and f(5)=5, then the probability that the function of type f:x→B where B⊆Y is of bijective in nature is
02:51View Solution