inside the circles x2+y2=1 there are three circles of equal radius a tangent to each other and to s the value of a equals to
√2(√2−1)
√3(2−√3)
√2(2−√3)
√3(√3−1)
The correct Answer is:B
To solve the problem of finding the radius a of three equal circles tangent to each other and to the larger circle defined by the equation x2+y2=1, we can follow these steps:
Step 1: Understand the Geometry
The larger circle has a radius of 1 (since x2+y2=1). The centers of the three smaller circles (each with radius a) will form an equilateral triangle, and each circle will be tangent to the larger circle and to each other.
Step 2: Determine the Distance Between Centers
The distance between the centers of any two smaller circles (say A and C) is equal to the sum of their radii:
AC=a+a=2a
Step 3: Relate the Centers to the Larger Circle
The distance from the center of the larger circle (point O) to the center of any smaller circle (point A or C) is:
OA=OC=1−a
This is because the distance from the center of the larger circle to the edge of the smaller circle is the radius of the larger circle minus the radius of the smaller circle.
Step 4: Use the Cosine Rule
In triangle OAC, we know that it is equilateral with angles of 120∘ between any two sides. Using the cosine rule:
AC2=OA2+OC2−2⋅OA⋅OC⋅cos(120∘)
Substituting the values:
(2a)2=(1−a)2+(1−a)2−2(1−a)(1−a)(−12)
Step 5: Simplify the Equation
Expanding the equation:
4a2=2(1−a)2+(1−a)2
4a2=2(1−2a+a2)+(1−2a+a2)
4a2=3(1−2a+a2)
4a2=3−6a+3a2
Step 6: Rearrange the Equation
Rearranging gives:
4a2−3a2+6a−3=0
a2+6a−3=0
Step 7: Apply the Quadratic Formula
Using the quadratic formula a=−b±√b2−4ac2a:
a=−6±√62−4⋅1⋅(−3)2⋅1
a=−6±√36+122
a=−6±√482
a=−6±4√32
a=−3±2√3
Step 8: Select the Positive Solution
Since a must be positive, we choose:
a=−3+2√3
Final Answer
Thus, the value of a is:
a=2√3−3
The larger circle has a radius of 1 (since x2+y2=1). The centers of the three smaller circles (each with radius a) will form an equilateral triangle, and each circle will be tangent to the larger circle and to each other.
The distance between the centers of any two smaller circles (say A and C) is equal to the sum of their radii:
AC=a+a=2a
The distance from the center of the larger circle (point O) to the center of any smaller circle (point A or C) is:
OA=OC=1−a
This is because the distance from the center of the larger circle to the edge of the smaller circle is the radius of the larger circle minus the radius of the smaller circle.
In triangle OAC, we know that it is equilateral with angles of 120∘ between any two sides. Using the cosine rule:
AC2=OA2+OC2−2⋅OA⋅OC⋅cos(120∘)
Substituting the values:
(2a)2=(1−a)2+(1−a)2−2(1−a)(1−a)(−12)
Expanding the equation:
4a2=2(1−a)2+(1−a)2
4a2=2(1−2a+a2)+(1−2a+a2)
4a2=3(1−2a+a2)
4a2=3−6a+3a2
Rearranging gives:
4a2−3a2+6a−3=0
a2+6a−3=0
Using the quadratic formula a=−b±√b2−4ac2a:
a=−6±√62−4⋅1⋅(−3)2⋅1
a=−6±√36+122
a=−6±√482
a=−6±4√32
a=−3±2√3
Since a must be positive, we choose:
a=−3+2√3
Thus, the value of a is:
a=2√3−3
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type9videos
CIRCLES
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE7videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - MATRIX MATCH TYPE9videos
COMPLEX NUMBERS
Similar Questions
Consider the circles x2+(y−1)2=9,(x−1)2+y2=25. They are such that these circles touch each other one of these circles lies entirely inside the other each of these circles lies outside the other they intersect at two points.
View Solution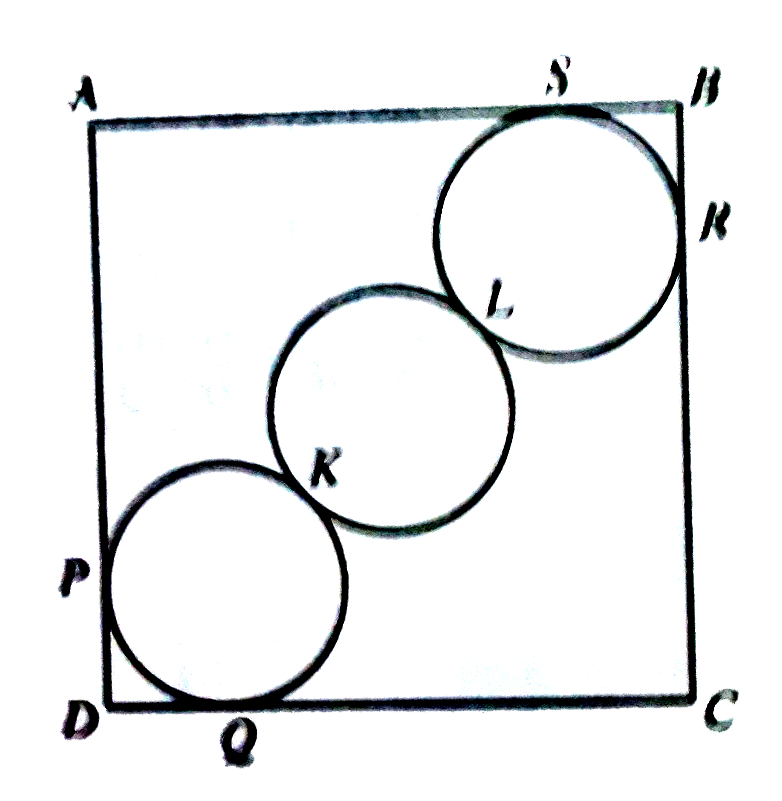
In the diagram above, ABCD is a square . The circles , whose centers lie on ¯¯¯¯¯¯BD, are congruent to each other . The sides of the square are tangent to the outer circles at P,Q,R and S , and the circles are tangent to each other at K and L . If the radius of each circle is 1 inch. What is the area , to the nearest square inch, of the square ?View SolutionThe point (1,4) are inside the circle S:x2+y2−6x−10y+k=0. What are the possible values of k if the circle S neither touches the axes nor cut them
View SolutionThe point P(−1,0) lies on the circle x2+y2−4x+8y+k=0. Find the radius of the circle Also determine the equation of the circle of equal radius which touches the given circle at P.
View SolutionThe focal chords of the parabola y2=16x which are tangent to the circle of radius r and centre (6, 0) are perpendicular, then the radius r of the circle is
View SolutionLet P and Q be 2 circles externally touhing each other at point X. Line segment AB is a direct common tangent to circle P and Q at points A and B respectively. Another common tangent to P and Q at X intersects line AB at a point Y. If BY = 10 units and the radius of P is 9 units, then the value of the reciprocal of the radius of the radius of the circle Q is equal to
View SolutionThe circle with centre (2,3) touching x-axis has the radius equal to
View SolutionTangents drawn from (2,0) to the circle x2+y2=1 touch the circle at AandB Then.
View SolutionWrite the equation of the circle having radius 5. and tangent as the line' 3x - 4y +5 = 0 at (1,2).
View SolutionWrite the equation of the circle having radius 5 and tangent as the line 3x−4y+5=0 at (1,2)
View Solution
