In the given figure, AD is the bisector of ∠BAC. If AB =10 cm , AC=6 cm and BC=12 cm, find BD and DC .
Let BD= x cm. then.
DC=(BC−BD)=(12−x)cm.
In ΔABC,AD is the bisector of ∠BAC.
So, by angle-bisector theorem, we have

BDDC=ABAC⇒x12−x=106
⇒6x=10(12−x)
⇒16x=120⇒x=7.5
Hence, BD=7.5cm,andDC=(12−7.5)cm,=4.5cm
Related Playlists
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE4videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
In the given figure , Ad is the bisector of ∠BAC. If AB = 10 cm , AC = 14 cm and BC = 8 cm , find BD and DC respectively .
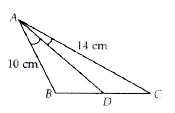 View Solution
View SolutionIn the given figure , if AD is the bisector of ∠BAC . If AB=10 cm , AC = 14 cm and BC = 6 cm , then find BD and DC .
 View Solution
View SolutionIn the given figure AD is the bisector of ∠A. If BD= 4 cm , DC = 3 cm and AB = 6cm . Find AC.
 View Solution
View SolutionIn figure AD is the bisector of ∠BAC. If BD=2cm,CD=3cmandAB=5cm. Find AC :
 View Solution
View SolutionIn the given figure, AD is the bisector of ∠BAC,AB=6cm,AC=5cm and BD=3cm, find DC.
 View Solution
View SolutionIn the figure, AD is the bisector of angle BAC. Prove that AB>BD.
View SolutionIn the given figure AC is bisector of ∠BAD, AB=3cm,AC=5cm, then AD= ______
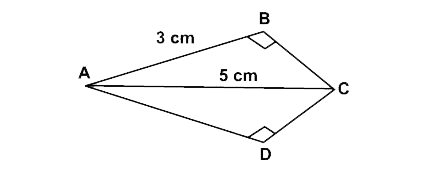 View Solution
View SolutionIn the figure , AD is bisector of ˆA . If BC = 10 cm , BD = 6 cm , and AC = 6 cm, find AB.
View SolutionIn Fig. 4.42, AD is the bisector of ∠BAC . If AB=10cm . AC=14cm and BC=6cm , find BD and DC . (FIGURE)
View SolutionIn a ΔABC,AD is the bisector of ∠A.
(i) If AB=6.4cm,AC=8cmandBD=5.6cm, find DC.
(ii) If AB=10cm,AC=14cmandBC=6cm, find BD and DC.
(iii) If AB=5.6cm,BD=3.2cm,andBC=6cm, find AC.
(iv) If AB=5.6cm,AC=4cm,andDC3cm, find BC.
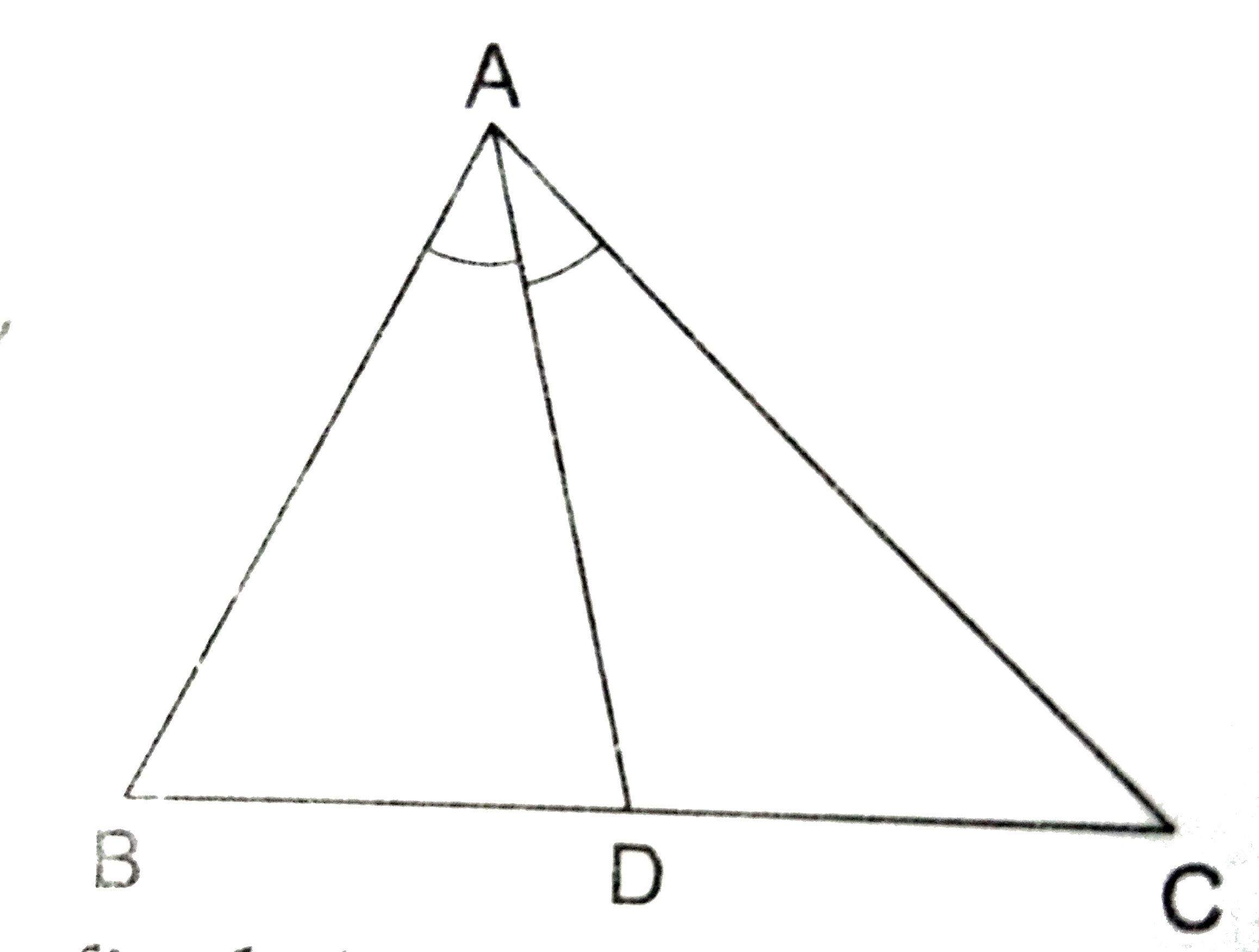 View Solution
View Solution


