In the adjoining figure. AD and BE are two medians of ΔABC. IfDF||BE,then prove thatCF=14AC.
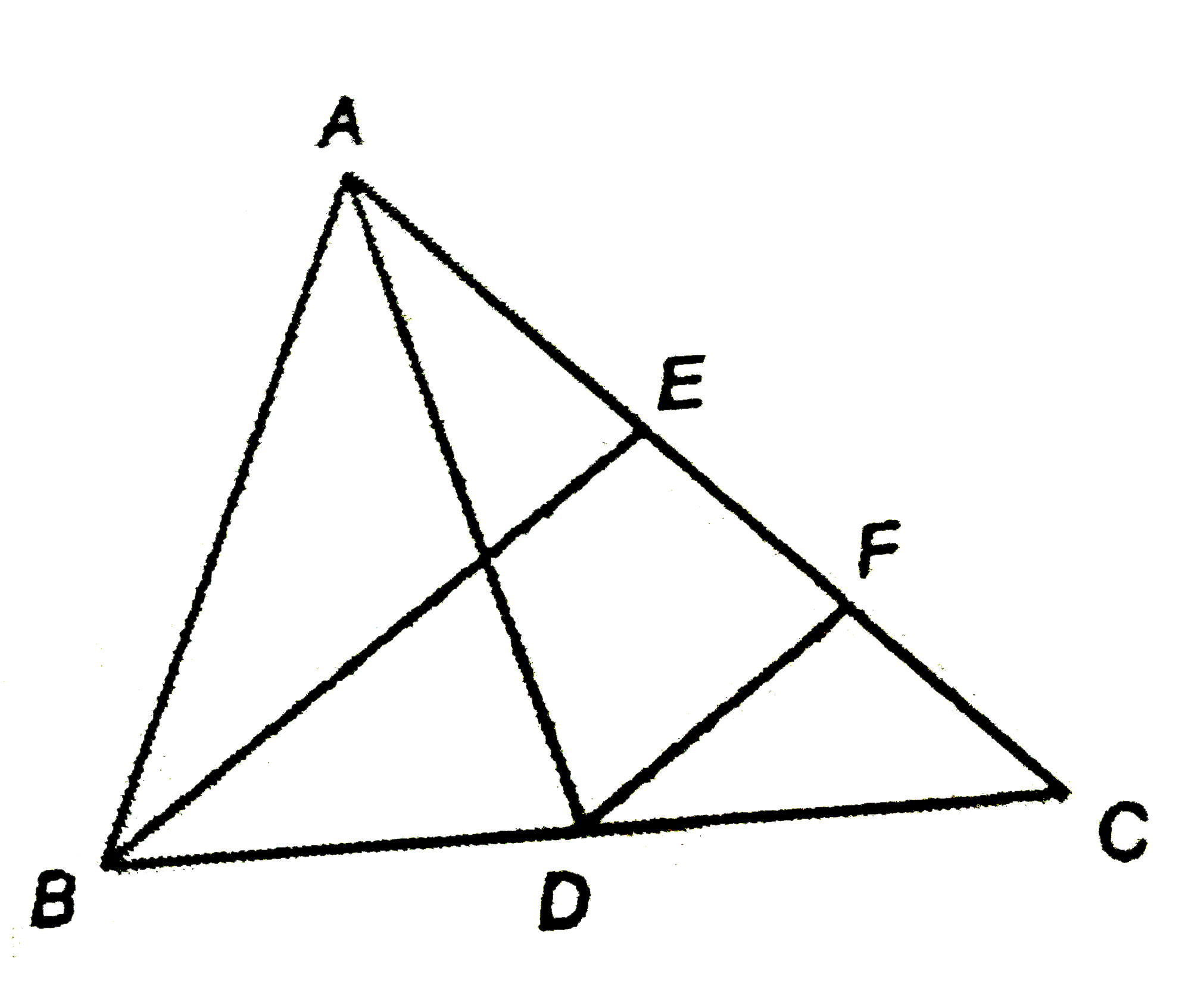
E is the mid-point of line AC.
∴CE=12AC ...(1)
In ΔABE,
Since, D is the mid-point of CB and DF||BE
∴F will be the mid-point of CE. (coverse of mid-point theorem)
⇒ CF=12CE
⇒ CF=12×12AC [from(1)]
⇒ CF=14AC
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:Revision Exercise
Explore 12 Videos
Similar Questions
In the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
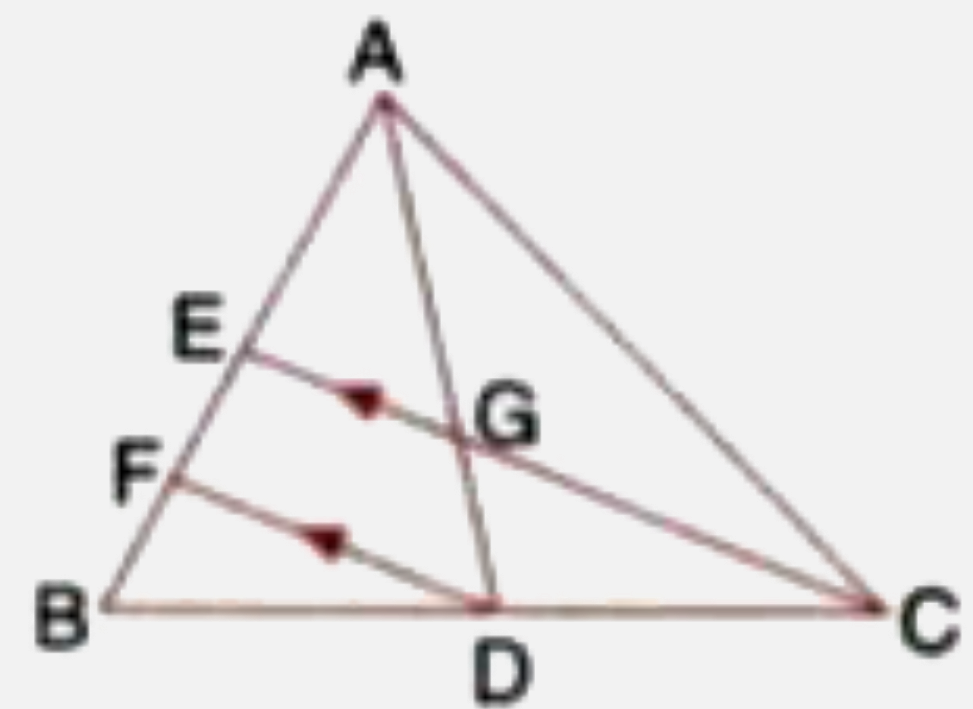
AG:GD=2:1.
View SolutionIn the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
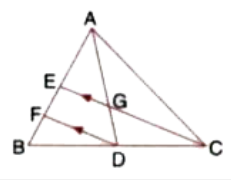
EF=FB
View SolutionFrom the adjoining figure, find the length of AC.

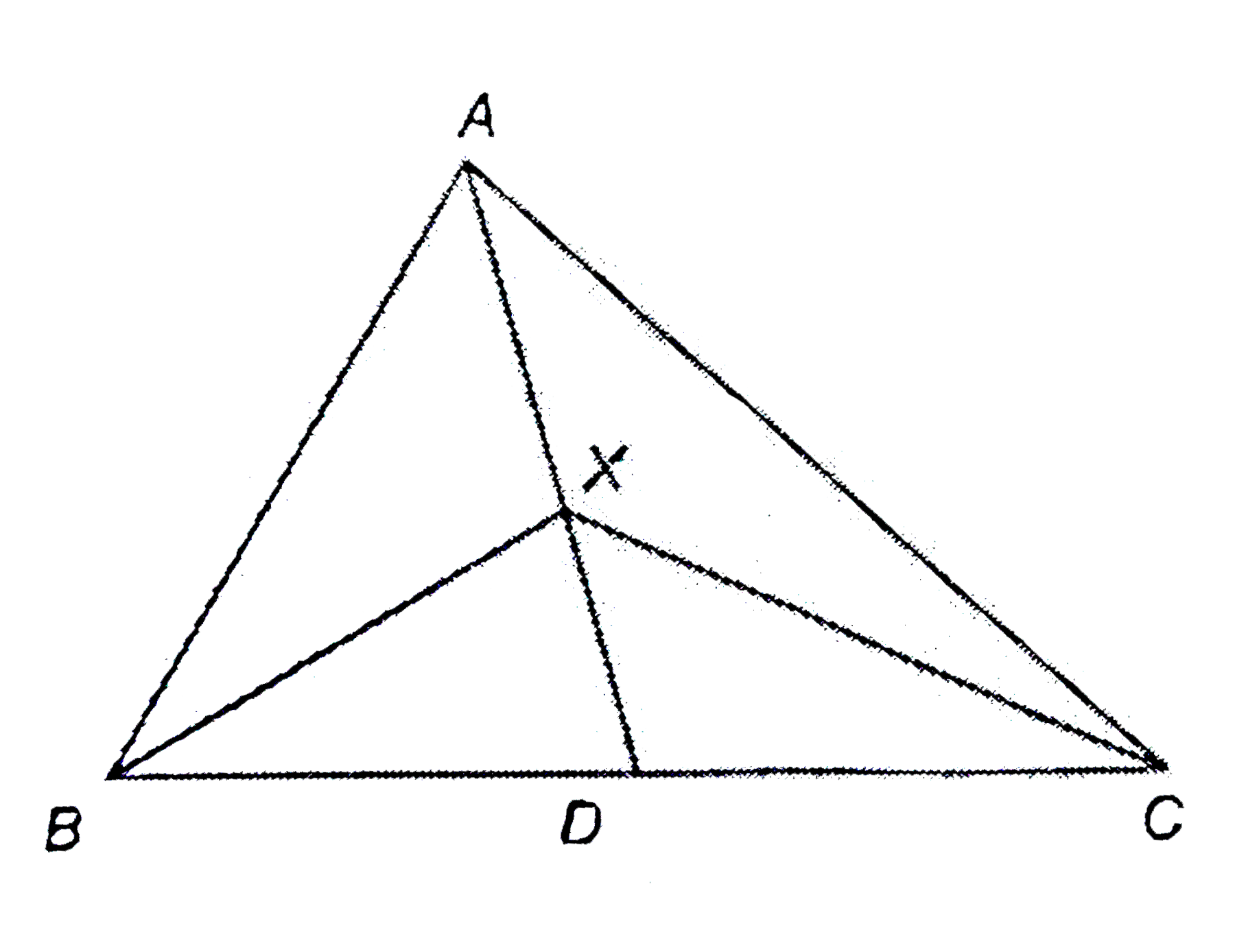
View SolutionIn the adjoining figure, AD is the median of ΔABC and X be any point on side AD. Prove that:
area (ΔABX)= area (ΔACX)
View SolutionIn the adjoining figure, P is an interior point of ΔABC. Then prove that :
AB+BC+CA<2(PA+PB+PC)

View SolutionIn the given figure, AD and CE are medians and DF∣∣CE. Prove that : FB=14AB.
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
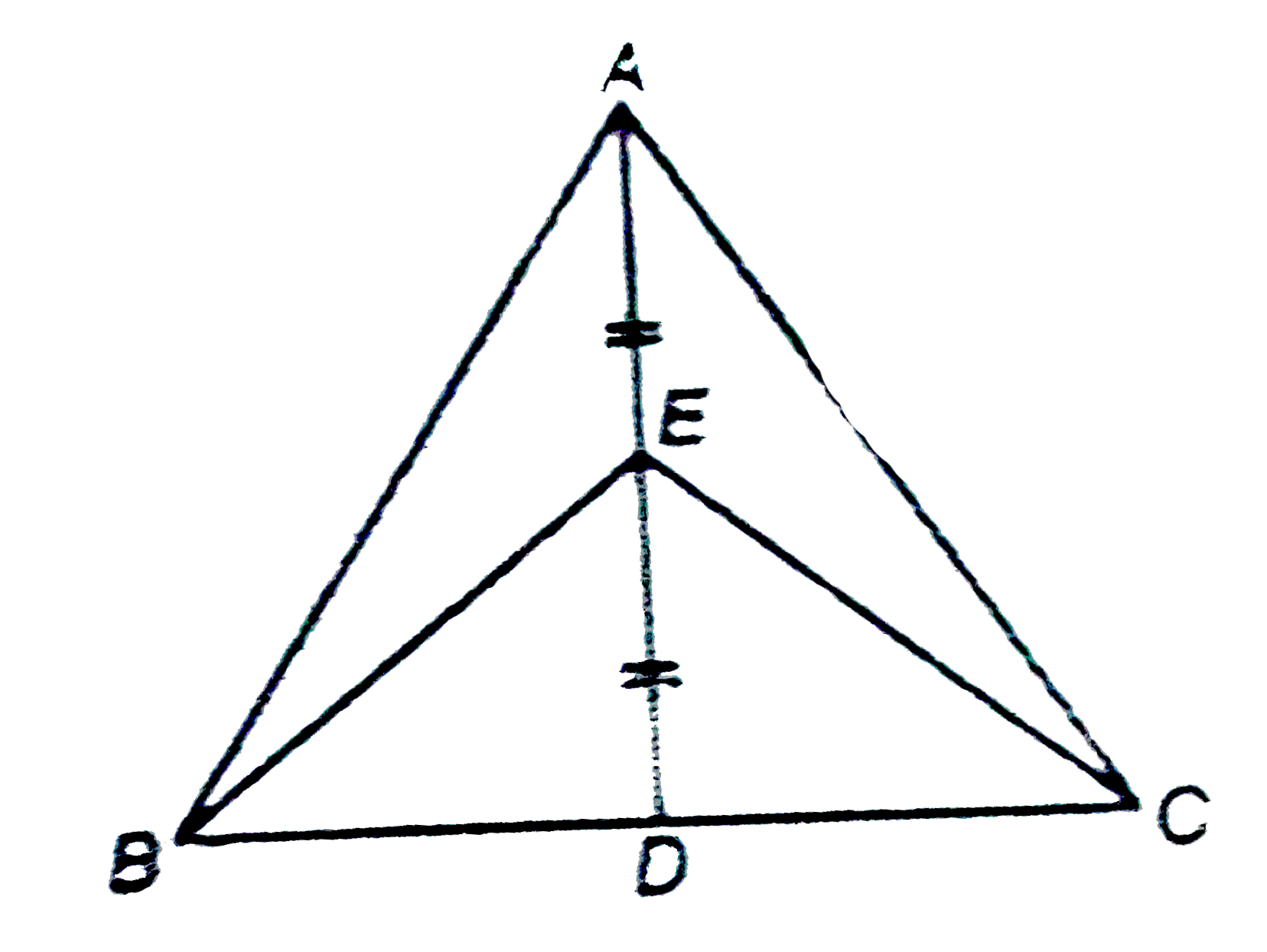
View SolutionIn the adjoining figure two medians AD and BE of a △ABC meet each other at O. prove that (i) △AOB~△DOE
View SolutionIn the following figure, BL = CM.
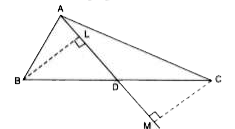
Prove that AD is a median of triangle ABC.
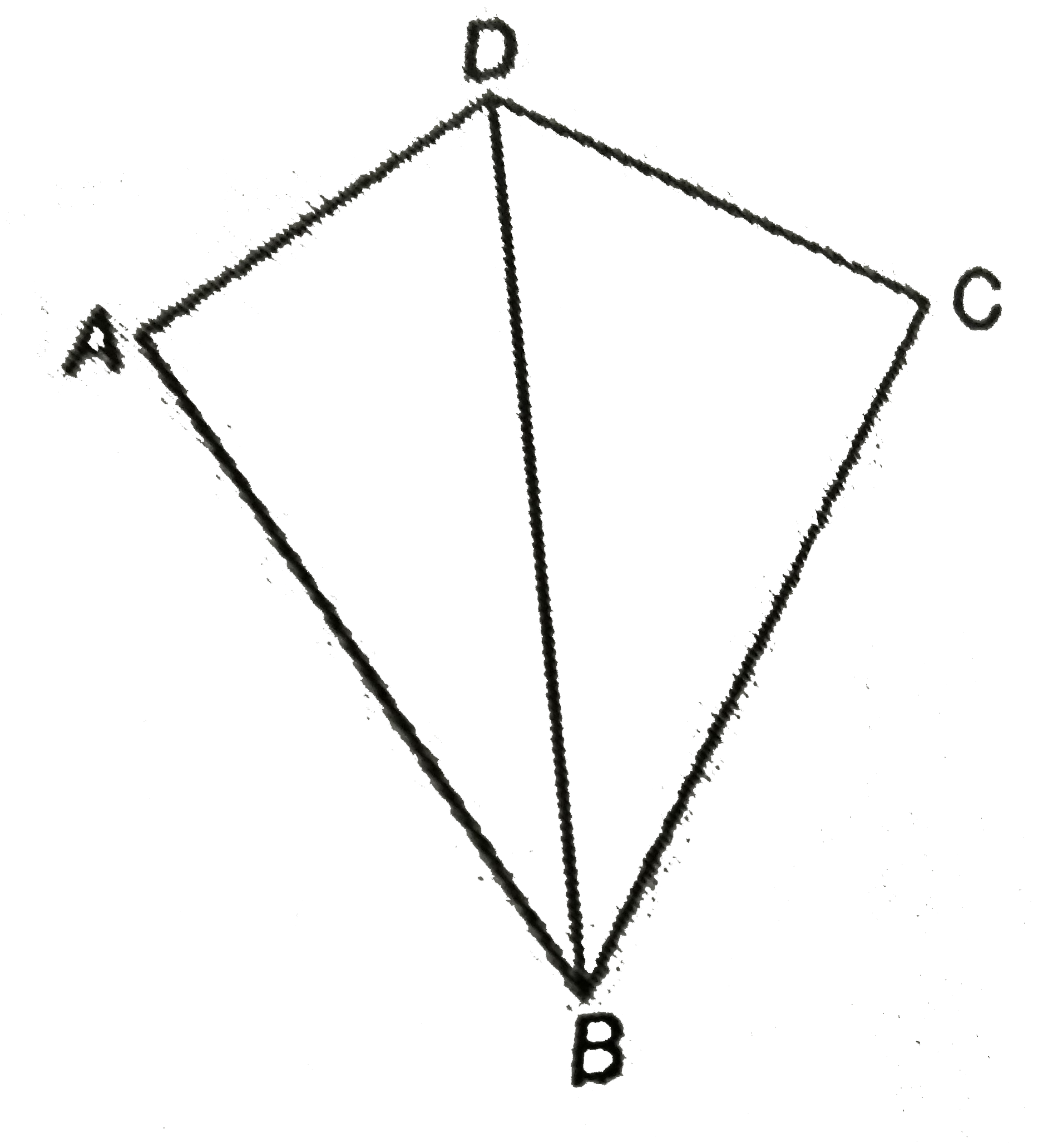
View SolutionIn the adjoining figure, AD=DC and DB bisects ∠ADC. Prove that ΔADB≅ΔCDB.
View Solution

