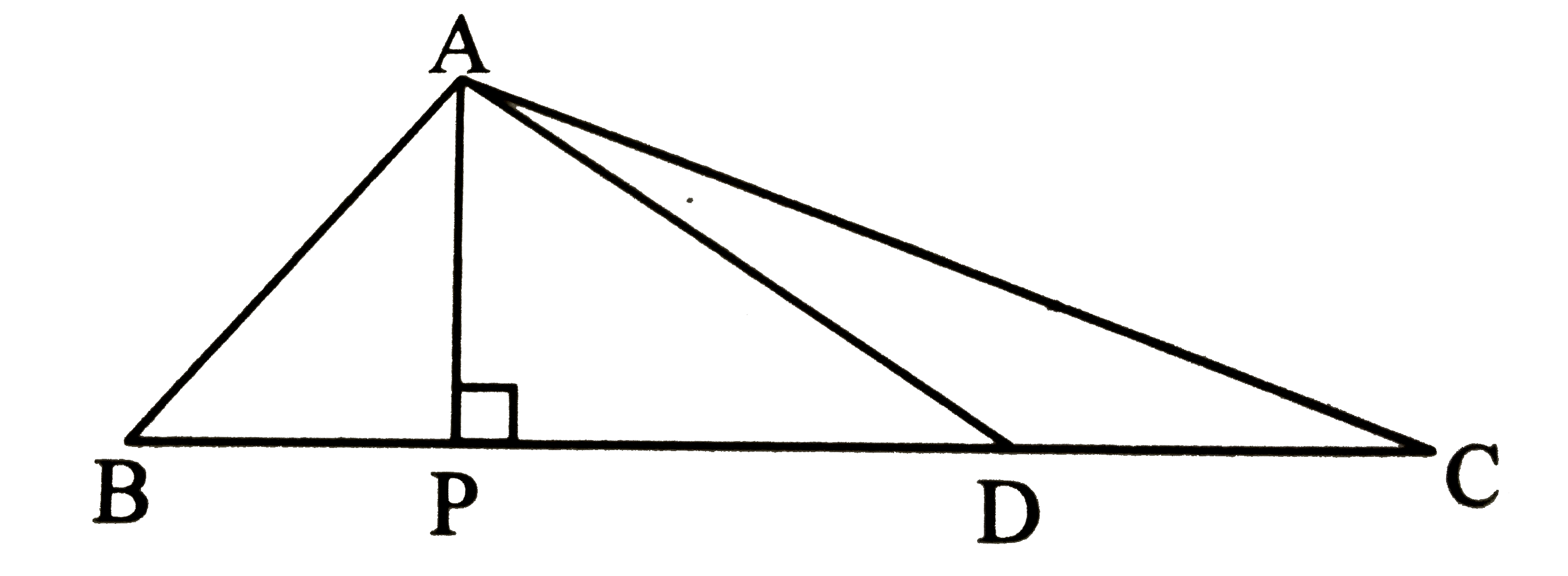
In ΔABC,point D is on side BC such that DC = 6, BC = 15. find
(i) A(ΔABD):A(ΔABC) and
(ii) A(ΔABD):A(ΔADC).
 Solution in Marathi
Solution in Marathi
Step by step video solution for In DeltaABC,point D is on side BC such that DC = 6, BC = 15. find (i) A(DeltaABD):A(DeltaABC) and (ii) A(DeltaABD):A(DeltaADC). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY Book:BAL BHARTIChapter:SIMILARITY Exercise:SOLVED EXAMPLES
Explore 3 Videos
- SIMILARITY Book:BAL BHARTIChapter:SIMILARITY Exercise:PRACTICE SET 1.1
Explore 3 Videos
- QUADRATIC EQUATIONSBook:BAL BHARTIChapter:QUADRATIC EQUATIONSExercise:Problem Set - 2
Explore 27 Videos
- TRIGONOMETRYBook:BAL BHARTIChapter:TRIGONOMETRYExercise:Problem set 6
Explore 18 Videos
Similar Questions
ΔABC~ΔPQR,A(ΔABC)=16,A(ΔPQR)=25, then infd the value of ration ABPQ.
View SolutionBase of a triangle is 9 cm and height is 5 cm. Base of another triangle is 10 cm and height is 6 cm. Find the ratio of areas of these triangles.
View SolutionWhich of the following equation is quadratic?
(i) x2+2x+11=0.
View SolutionIf sinθ = 11/61 find the values of cosθ using trigonometric identity.
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn ΔABC,B−D−C and BD=7,BC=20, then find followig ratios:
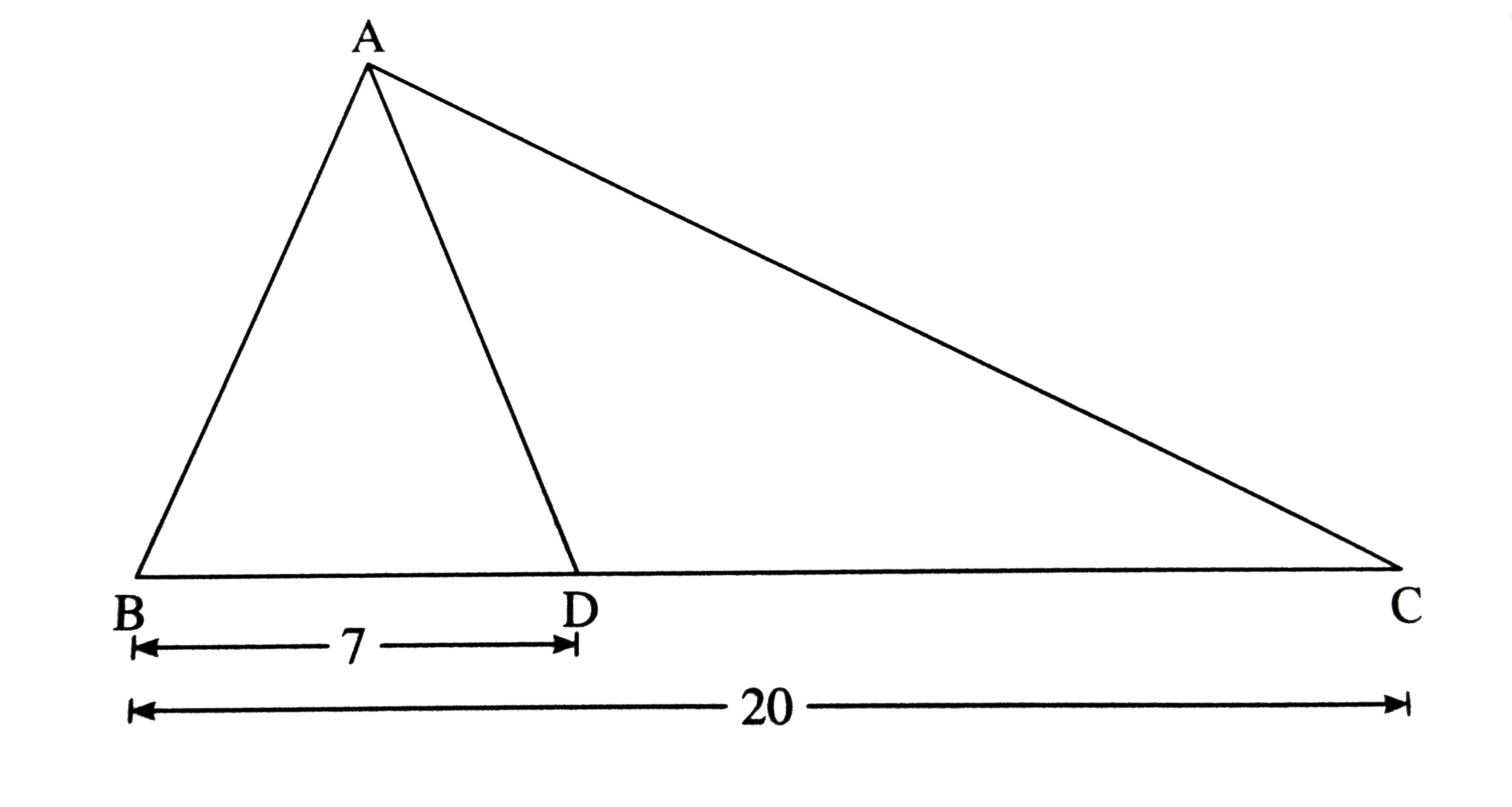
A(ΔABD)A(ΔADC)
A(ΔABD)A(ΔABC)
A(ΔADC)A(ΔABC)
View SolutionIn ΔABC,point D is on side BC such that DC = 6, BC = 15. find
(i)A(ΔABD):A(ΔABC) and
(ii) A(ΔABD):A(ΔADC).

View SolutionD is any point on the side BC of ΔABC. P and Q are centroids of ΔABD and ΔADC respectively. Prove that PQ∣∣BC.
View Solution

