In a triangle XYZ, let x, y, z be the lengths of sides opposite to the angles X, Y, Z, respectively, and 2s = x + y + z. If s−x4=s−y3=s−z2 of incircle of the triangle XYZ is 8π3
(a) area of the triangle XYZ is 6√6
(b) the radius of circumcircle of the triangle XYZ is 356√6
(c) sin.X2sin.Y2sin.Z2=435
(d) sin2(X+Y2)=35
The correct Answer is:A, C, D
To solve the problem step by step, we will follow the given conditions and derive the necessary values.
Step 1: Understand the given conditions
We have a triangle XYZ with sides opposite to angles X, Y, and Z denoted as x, y, and z respectively. The semi-perimeter s is given by:
2s=x+y+z
We also have the condition:
s−x4=s−y3=s−z2=λ
where λ is a constant.
Step 2: Express the sides in terms of λ
From the equations, we can express s−x, s−y, and s−z in terms of λ:
s−x=4λ⇒x=s−4λ
s−y=3λ⇒y=s−3λ
s−z=2λ⇒z=s−2λ
Step 3: Substitute into the semi-perimeter equation
Now, substituting x, y, and z into the semi-perimeter equation:
x+y+z=(s−4λ)+(s−3λ)+(s−2λ)=3s−9λ
Since 2s=x+y+z:
2s=3s−9λ
Rearranging gives:
s=9λ
Step 4: Find the lengths of the sides
Now that we have s, we can find x, y, and z:
x=s−4λ=9λ−4λ=5λ
y=s−3λ=9λ−3λ=6λ
z=s−2λ=9λ−2λ=7λ
Step 5: Find the area using Heron's formula
The area A of the triangle can be calculated using Heron's formula:
A=√s(s−x)(s−y)(s−z)
Substituting the values:
A=√9λ⋅(9λ−5λ)⋅(9λ−6λ)⋅(9λ−7λ)
=√9λ⋅4λ⋅3λ⋅2λ=√24⋅9λ4=6√6λ2
Step 6: Relate the area to the radius of the incircle
The area of the triangle can also be expressed in terms of the radius r of the incircle:
A=r⋅s
Given that the area is 8π3:
6√6λ2=r⋅9λ
Thus:
r=6√6λ29λ=2√63λ
Step 7: Solve for λ
Since the area is given as 8π3, we can set up the equation:
6√6λ2=8π3
Solving for λ2:
λ2=8π18√6=4π9√6
Step 8: Final calculations
Now substituting back to find r:
r=2√63⋅√4π9√6=2√63⋅2√π3√(4)6=4√π9
Conclusion
The radius of the incircle and the area of the triangle have been calculated based on the given conditions.
We have a triangle XYZ with sides opposite to angles X, Y, and Z denoted as x, y, and z respectively. The semi-perimeter s is given by:
2s=x+y+z
We also have the condition:
s−x4=s−y3=s−z2=λ
where λ is a constant.
From the equations, we can express s−x, s−y, and s−z in terms of λ:
s−x=4λ⇒x=s−4λ
s−y=3λ⇒y=s−3λ
s−z=2λ⇒z=s−2λ
Now, substituting x, y, and z into the semi-perimeter equation:
x+y+z=(s−4λ)+(s−3λ)+(s−2λ)=3s−9λ
Since 2s=x+y+z:
2s=3s−9λ
Rearranging gives:
s=9λ
Now that we have s, we can find x, y, and z:
x=s−4λ=9λ−4λ=5λ
y=s−3λ=9λ−3λ=6λ
z=s−2λ=9λ−2λ=7λ
The area A of the triangle can be calculated using Heron's formula:
A=√s(s−x)(s−y)(s−z)
Substituting the values:
A=√9λ⋅(9λ−5λ)⋅(9λ−6λ)⋅(9λ−7λ)
=√9λ⋅4λ⋅3λ⋅2λ=√24⋅9λ4=6√6λ2
The area of the triangle can also be expressed in terms of the radius r of the incircle:
A=r⋅s
Given that the area is 8π3:
6√6λ2=r⋅9λ
Thus:
r=6√6λ29λ=2√63λ
Since the area is given as 8π3, we can set up the equation:
6√6λ2=8π3
Solving for λ2:
λ2=8π18√6=4π9√6
Now substituting back to find r:
r=2√63⋅√4π9√6=2√63⋅2√π3√(4)6=4√π9
The radius of the incircle and the area of the triangle have been calculated based on the given conditions.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Archives (Matrix Match Type)
Explore 1 Video
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Archives (Numerical Value Type)
Explore 3 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGE ENGLISHChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Archives (JEE Advanced)
Explore 3 Videos
- PROGRESSION AND SERIESBook:CENGAGE ENGLISHChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- RELATIONS AND FUNCTIONSBook:CENGAGE ENGLISHChapter:RELATIONS AND FUNCTIONSExercise:Archives(Matrix Match Type)
Explore 1 Video
Similar Questions
In a triangle △XYZ, let a,b,c be the lengths o the sides opposite to the angle X,Y and Z respectively. If 1+cos2X−2cos2Y=2sinXsinY, then positive value (s) of ab is (are
View SolutionIf s−x/4= s−y/3=s-z/2 and area of incircle of the triangle XYZ is 8(pi)/3 thenThe radius of the circumcircle of △XYZ
View Solution
Knowledge Check
In triangle PQR. ∠Q is a right angle, QR=24, and PR=26. Triangle YXZ is similar to triangle PQR, where vertices X, Y, and Z correspond to vertices P, Q, and R, respectively, and each side of triangle XYZ is 12 the length of the corresponding side of triangle PQR. What is the value of sin Z?
A513B512C1213D125
In a ΔPQR (as shown in figure) if x:y:z=2:3:6, then the value of ∠QPR is :
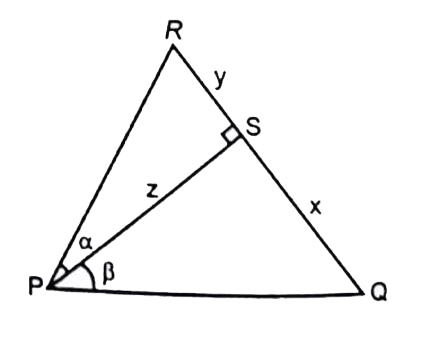
View SolutionIf in ΔABC, the distance of the vertices from the orthocenter are x,y, and z then prove that ax+by+cz=abcxyz
View SolutionIn a ΔPQR as show in figure given that x:y:z::2:3:6, then find value of ∠QPR.
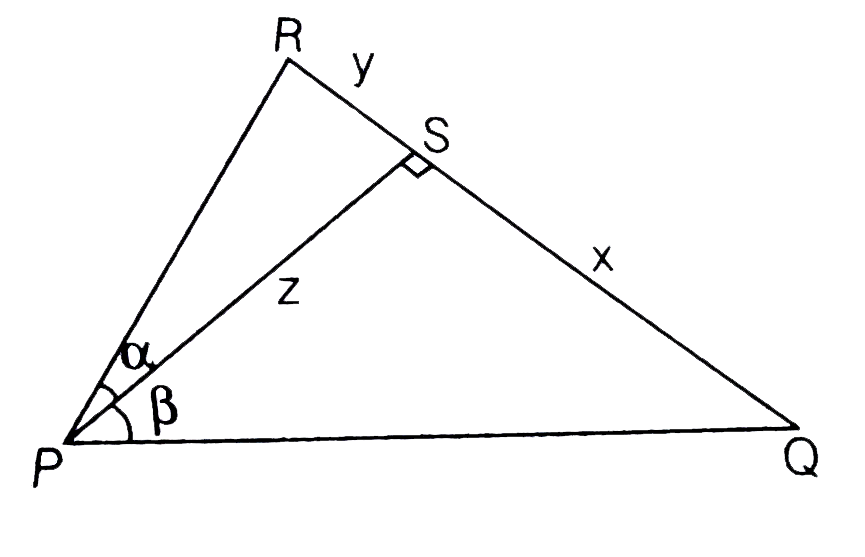
View SolutionFind the perimeter of a triangle whose sides are 2y+3z,z−y,4y−2z.
View SolutionLet x,y,z are positive reals and x+y+z=60andx>3.
Maximum value of xyz is :
View SolutionFind the coordinates of the centroid of the triangle whose vertices are (x1,y1,z1), (x2,y2,z2)and (x3,y3,z3).
View SolutionIf xyz=1 and x,y,z>0 then the minimum value of the expression (x+2y)(y+2z)(z+2x) is
View Solution

