In a triangle PQR,SandT are points on QRandPR, respectively, such that QS=3SRandPT=4TR. Let M be the point of intersection of PSandQT. Determine the ratio QM:MT using the vector method .
The correct Answer is:15:4

Let QM:MT=λ:1andPM:MS=μ:1
and −−→QP=→a,−−→QP=→b
⇒ −−→QT=4→b+→a5
and −−→QM=λλ+1(4→b+→a5) (i)
−−→QS=34→b,−−→QM=μ(34→b)+→aμ+1 (ii)
From (i) and (ii), we have
1μ+1=λ5(λ+1)and4λ5(λ+1)=3μ4(μ+1)
⇒λ=15/4andμ=16/3
∴ QM:MT=15:4
Topper's Solved these Questions
- INTRODUCTION TO VECTORS Book:CENGAGEChapter:INTRODUCTION TO VECTORS Exercise:Exercise (Single)
Explore 34 Videos
- INTRODUCTION TO VECTORS Book:CENGAGEChapter:INTRODUCTION TO VECTORS Exercise:Exercise (Multiple)
Explore 13 Videos
- INTRODUCTION TO VECTORS Book:CENGAGEChapter:INTRODUCTION TO VECTORS Exercise:Exercise 1.2
Explore 7 Videos
- INTEGRALSBook:CENGAGEChapter:INTEGRALSExercise:Solved Examples And Exercises
Explore 324 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:Question Bank
Explore 24 Videos
Similar Questions
In a triangle PQR,SandT are points on QRandPR, respectively, such that QS=3SRandPT=4TR. Let M be the point of intersection of PSandQT. Determine the ratio QM:MT using the vector method .
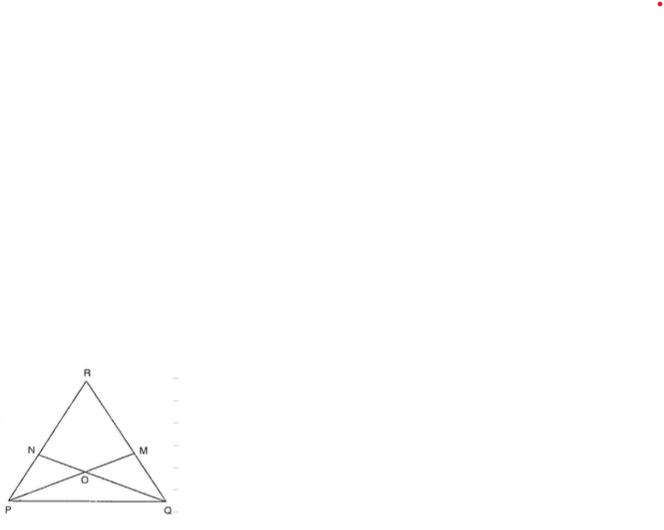
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View SolutionIn a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC=21 cm, BC=29cm and AB=30cm, find the perimeter of the quadrilateral ARPQ
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionOPQR is a square and M,N are the middle points of the sides PQandQR , respectively. Then the ratio of the area of the square to that of triangle OMN is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
View Solution

