If the eccentric angles of two points P and Q on the ellipse x228+y27=1 whose centre is C differ by a right angle then the area of ΔCPQ is
5
6
7
8
The correct Answer is:C
If P is the point (acosθ,bsinθ), the coordinates of Q are (acos(θ+π2),bsin(θ+π2))
i.e., (−asinθ,bcosθ) where a2=28,b2=7
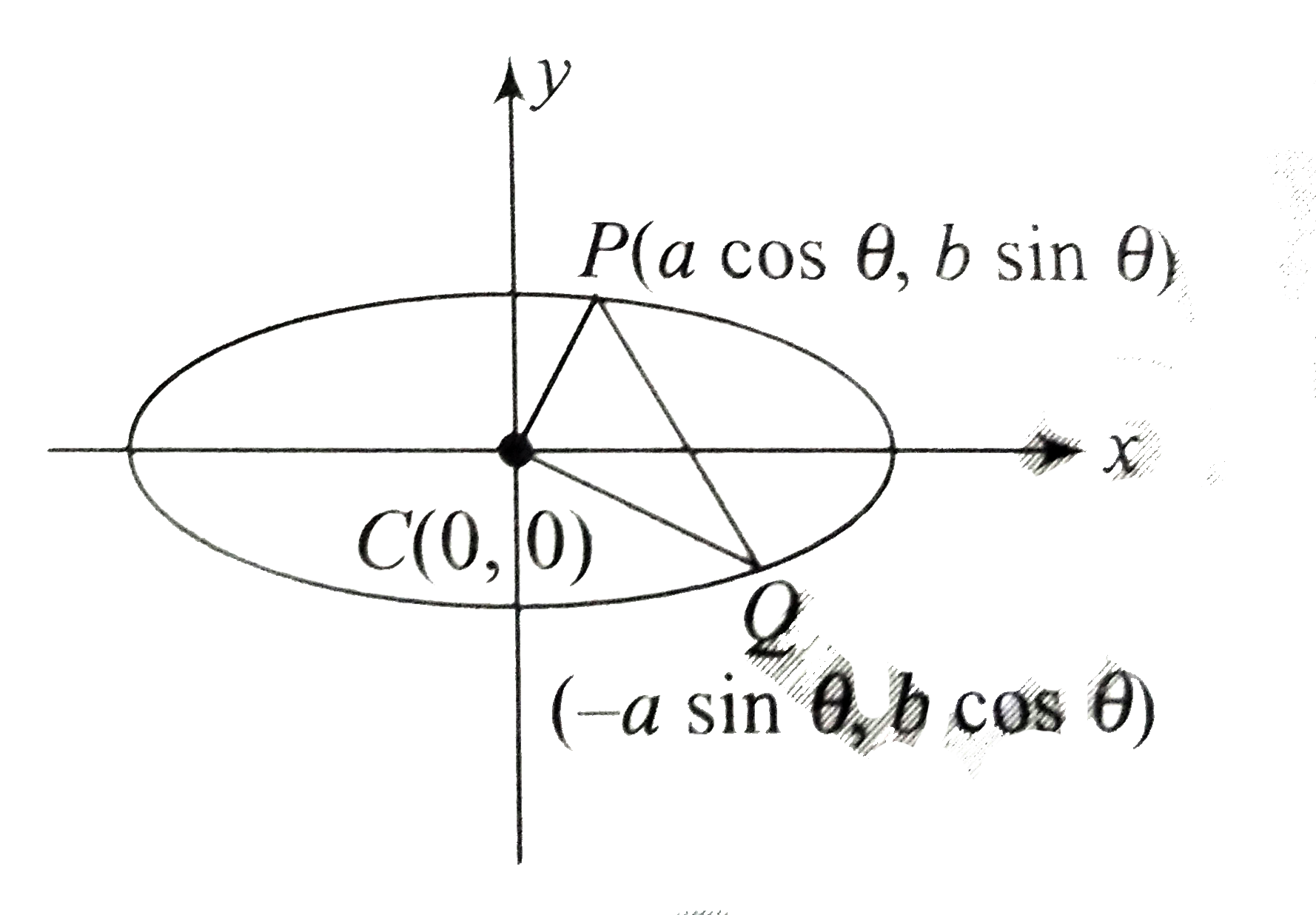
∴ The area of ΔCPQ=12∣∣abcos2θ+absin2θ∣∣{∵area=∣∣∣{12(x1y2−x2y2)}∣∣∣}
=12ab
=12(√28)(√7)=7 sq units.
Topper's Solved these Questions
- ELLIPSE Book:CENGAGE ENGLISHChapter:ELLIPSE Exercise:Single Correct Answer Type
Explore 49 Videos
- DOT PRODUCTBook:CENGAGE ENGLISHChapter:DOT PRODUCTExercise:DPP 2.1
Explore 15 Videos
- EQAUTION OF STRAIGHT LINE AND ITS APPLICATION Book:CENGAGE ENGLISHChapter:EQAUTION OF STRAIGHT LINE AND ITS APPLICATION Exercise:DPP 3.2
Explore 13 Videos
Similar Questions
The eccentric angle of a point on the ellipse x26+y22=1 whose distance from the centre of the ellipse is 2, is
View SolutionFind the eccentric angle of a point on the ellipse x26+y22=1 whose distance from the center of the ellipse is √5
View SolutionFind the eccentric angle of a point on the ellipse x26+y22=1 whose distance from the center of the ellipse is √5
View SolutionP and Q are two points on the ellipse x2a2+y2b2=1 whose eccentric angles are differ by 90∘, then
View SolutionThe eccentric angles of the ends of L.R. of the ellipse (x2a2)+(y2b2)=1 is
View SolutionEccentric angle of a point on the ellipse x24+y23=1 at a distance 2 units from the centre of ellipse is:
View SolutionIf the tangents from the point (λ,3) to the ellipse x29+y24=1 are at right angles then λ is
View SolutionArea of the triangle formed by the tangents at the point on the ellipse x2a2+y2b2=1 whose eccentric angles are α,β,γ is
View SolutionThe eccentric angles of the vertices of a triangle inscribed in the ellipse x2a2+y2b2=1 are α,β,γ, then for the area of this triangle to be greatest, the angle subtended by the two consecutive vertices of the triangle at the centre of the ellipse in degree measure is...
View SolutionIf theta is the difference of the eccentric angles of two points on an ellipse, the tangents at which are at right angles. Prove that absinθ=d1d2, where d1,d2 are the semi diameters parallel to the tangents at the points and a,b are the semi-axes of the ellipse.
View Solution

