Question

If the eccentric angles of two points P and Q on the ellipse $\frac{x^2}{28}+\frac{y^2}{7}=1$ whose centre is C differ by a right angle then the area of $\Delta CPQ$ is

Options

A. 5
B. 6
C. 7
D. 8

Answer

C

Explanation

If P is the point `(a cos theta, b sin theta)`, the coordinates of Q are `(a cos (theta+ (pi)/(2)), b sin (theta + (pi)/(2)))`
i.e., `(-a sin theta, b cos theta)` where `a^(2) = 28, b^(2) =7`

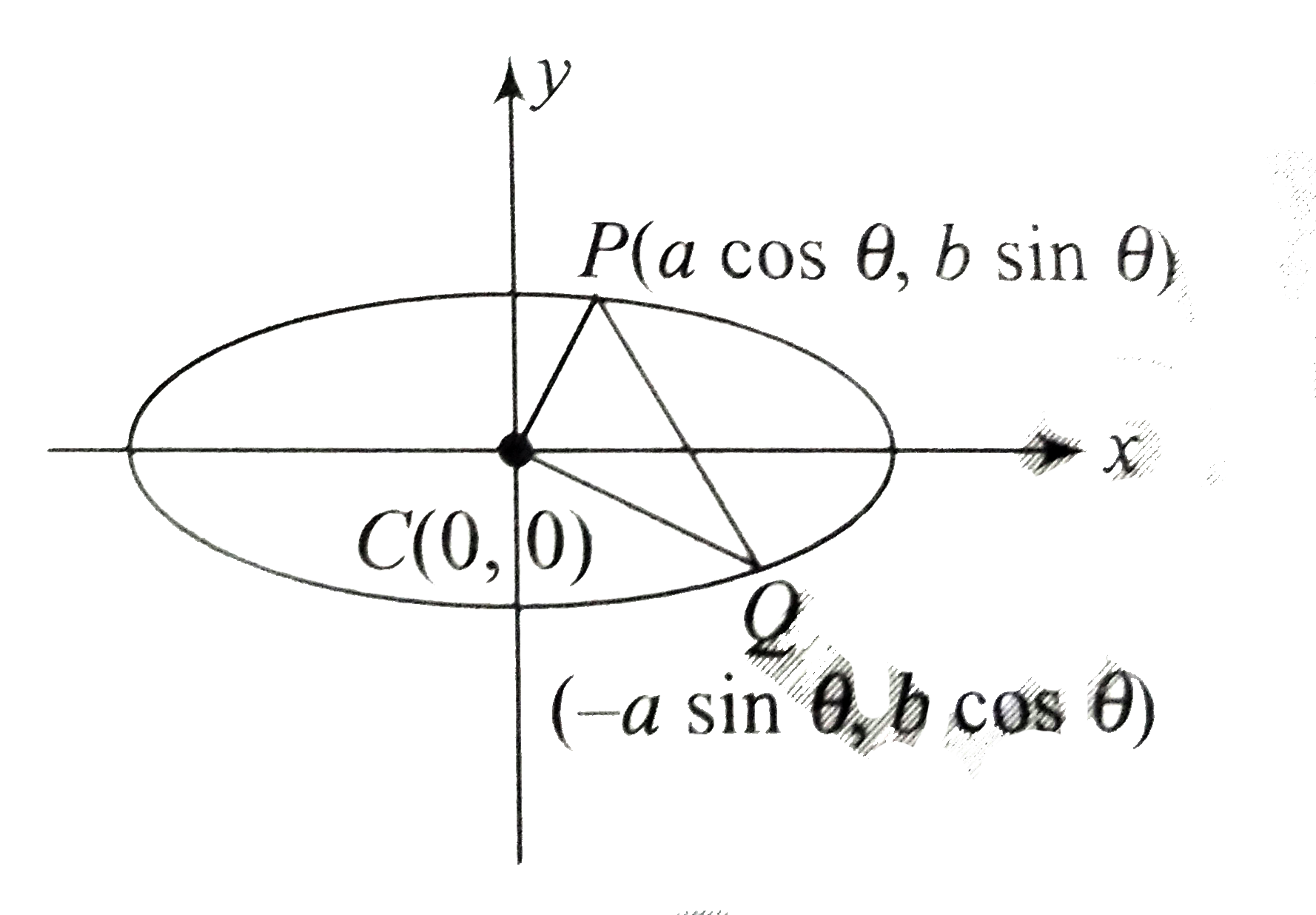
`:.` The area of `Delta CPQ = (1)/(2) |ab cos^(2) theta + ab sin^(2) theta| { :' area = |{(1)/(2)(x_(1)y_(2)-x_(2)y_(2))}|}`
`= (1)/(2)ab`
`= (1)/(2) (sqrt(28)) (sqrt(7)) =7` sq units.