If hyperbola passes through the foci of the ellipse . Its transverse and conjugate axes coincide respectively with the major and minor axes of the ellipse and if the product of eccentricities of hyperbola and ellipse is 1 then the equation of hyperbola is b. the equation of hyperbola is c. focus of hyperbola is (5, 0) d. focus of hyperbola is Solution in Tamil
the equation of hyperbola is
the equation of the hyperbola is
the vertex of the hyperbola is (5, 0)
the vertex of the hyperbola is
The correct Answer is:A, C
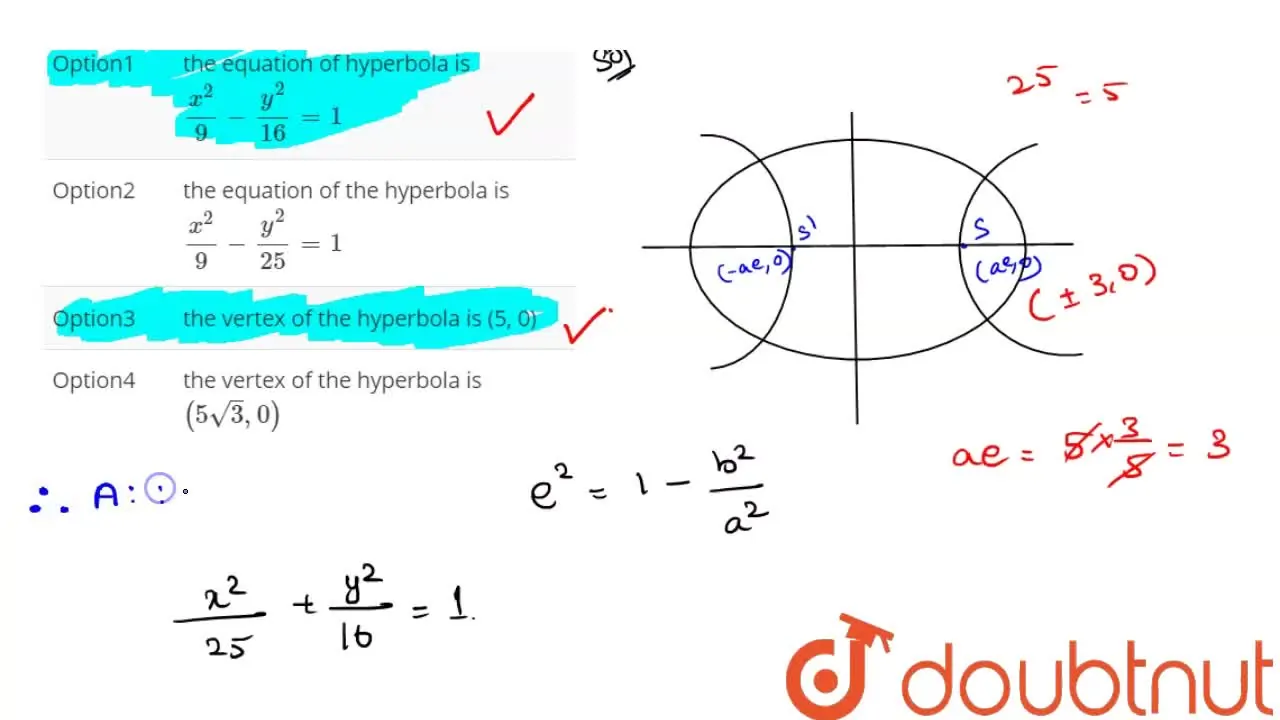
for given ellipse
we have
Hence, the eccentricity of the hyperbola is .
Let the hyperbola be
Then
Therefore, the equation of the hyperbola is
As it passes through (3, 0), we get
The equation is
The foci of the hyperbola are
The vertex of the hyperbola is (3, 0).
Related Playlists
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Comprehension)21videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Matrix)5videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Single)68videos
HYPERBOLA
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
- BOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Question Bank21videos
INDEFINITE INTEGRATION
Similar Questions
Consider an ellipse x2a2+y2b2=1(a>b). A hyperbola has its vertices at the extremities of minor axis of the ellipse and the length of major axis of the ellipse is equal to the distance between the foci of hyperbola. Let e1 and e2 be the eccentricities of ellipse and hyperbola, respectively. Also, let A1 be the area of the quadrilateral fored by joining all the foci and A2 be the area of the quadrilateral formed by all the directries.
If the tangent drawn at a point P on ellipse passes thorugh the focus hyperbola, then the eccentric angle of point P is (P lies in 1st quadrant)03:55View SolutionThe area enclosed by the ellipse x2a2+y2b2=1 is equal to
03:32View SolutionIf the distance between the foci and the distance between the two directricies of the hyperbola x2a2−y2b2=1 are in the ratio 3:2, then b:a is 1:√2 (b) √3:√2 1:2 (d) 2:1
03:44View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
04:39View SolutionLet k(x)=(x2+1)3√x3+3x+6dx and k(-1) = 1/root (3)(2)) then the value of k(-2) is
04:37View SolutionIf a hyperbola passes through the foci of the ellipse x225+y216=1 . Its transverse and conjugate axes coincide respectively with the major and minor axes of the ellipse and if the product of eccentricities of hyperbola and ellipse is 1 then the equation of a. hyperbola is x29−y216=1 b. the equation of hyperbola is x29−y225=1 c. focus of hyperbola is (5, 0) d. focus of hyperbola is (5√3,0)
06:57View SolutionA hyperbola passes through a focus of the ellipse (x^(2))/(169)+(y^(2))/(25)=1. Its transverse and conjugate axes coincide respectively with the major and minor axes of the ellipse.The product of eccentricities is 1. Then the equation of the hyperbola is
05:03View SolutionAn ellipse passes through a focus of the hyperbola x29−y216=1 and its major and minor axes coincide with the transverse and conjugate axes of the hyperbola and the product of eccentricities of ellipse and hyperbola is 1. Equation of ellipse is : (A) x216+y29=1 (B) x225+y29=1 (C) x225+y216=1 (D) none of these
View SolutionAn ellipse passes through a focus of the hyperbola x29−y216=1 and its major and minor axes coincide with the transverse and conjugate axes of the hyperbola and the product of eccentricities of ellipse and hyperbola is 1. Foci of the ellipse are (A) (±4,0) (B) (±3,0) (C) (±5,0) (D) none of these
View SolutionLet a hyperbola passes through the focus of the ellipse x225+y216=1. The transverse and conjugate axes of this hyperbola coincide with the major and minor axes of the given ellipse, also the product of eccentricities of given ellipse and hyperbola is 1, then
03:40View SolutionA hyperbola passes through a focus of the ellips x2169+y225=1. Its transverse and conjugates axes coincide respectively with the major and minor axes of the ellips The product of eccetricities is 1. Then the equation of the hyperbola is
05:11View SolutionIf a hyperbola passes through the focus of the ellipse x225+y216=1 and its transverse and conjugate gate axis coincides with the major and minor axis of the ellipse, and product of their eccentricities is 1, then
05:19View SolutionA hyperbola passing through a focus of the ellipse x2169+y225=1. Its transverse and conjugate axes coincide respectively with the major and minor axes of the ellipse. The product of eccentricities is 1. Then, the equation of the hyperbola is,
03:10View SolutionIf a hyperbola passes through a focus of the ellipse and it transverse and conjugate axes coincides with major and minor axis of the ellipse and the product of their eccentricities is 1, then
(i) Show that the equation of the hyperbola is x29−y216=1
(ii) Find the focus of the hyperbola.06:00View SolutionIf a hyperbola passes through the foci of the ellipse x225+y216=1 . Its transverse and conjugate axes coincide respectively with the major and minor axes of the ellipse and if the product of eccentricities of hyperbola and ellipse is 1 then the equation of a. hyperbola is x29−y216=1 b. the equation of hyperbola is x29−y225=1 c. focus of hyperbola is (5, 0) d. focus of hyperbola is (5√3,0)
06:41View SolutionIf a hyperbola passes through the foci of the ellipse x225+y216=1 . Its transverse and conjugate axes coincide respectively with the major and minor axes of the ellipse and if the product of eccentricities of hyperbola and ellipse is 1 then the equation of a. hyperbola is x29−y216=1 b. the equation of hyperbola is x29−y225=1 c. focus of hyperbola is (5, 0) d. focus of hyperbola is (5√3,0)
08:01View Solution