If (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then e=√38612 (b) e=√38613 LR=1216 (d) LR=1213Solution in Tamil
e=√38612
e=√38613
LR=121/6
LR=121/3
The correct Answer is:A, C
We have foci S1(5,12)andS2(24,7).
Hyperbola passes through P(0, 0).
∴ |PS1−PS2|=2a
2a=K
or 2a=∣∣∣√(24−0)2+(7−0)2−√122+52∣∣∣=12
∴ a=6
S1S2=2ae=√(24−5)2+(12−7)2=√386
∴ e=√38612
LR=2b2a=2a2(e2−1)a
=2×6(386144−1)=1216
Topper's Solved these Questions
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Comprehension)
21 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Matrix)
5 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - Exercise (Single)
68 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGECHAPTER - INDEFINITE INTEGRATIONEXERCISE - Question Bank
21 Videos
Similar Questions
Consider an ellipse x2a2+y2b2=1(a>b). A hyperbola has its vertices at the extremities of minor axis of the ellipse and the length of major axis of the ellipse is equal to the distance between the foci of hyperbola. Let e1 and e2 be the eccentricities of ellipse and hyperbola, respectively. Also, let A1 be the area of the quadrilateral fored by joining all the foci and A2 be the area of the quadrilateral formed by all the directries.
If the tangent drawn at a point P on ellipse passes thorugh the focus hyperbola, then the eccentric angle of point P is (P lies in 1st quadrant)
View SolutionThe area enclosed by the ellipse x2a2+y2b2=1 is equal to
View SolutionIf the distance between the foci and the distance between the two directricies of the hyperbola x2a2−y2b2=1 are in the ratio 3:2, then b:a is 1:√2 (b) √3:√2 1:2 (d) 2:1
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionLet k(x)=(x2+1)3√x3+3x+6dx and k(-1) = 1/root (3)(2)) then the value of k(-2) is
View SolutionA hyperbola passes through the point P(sqrt(2),sqrt(3)) and has foci at (+-2,0) them the tangent to this hyperbola at P also passes through the point (A)(sqrt(3),sqrt(2))(B)(-sqrt(2),-sqrt(3))(C)(3sqrt(2),2sqrt(3))(D)(2sqrt(2),3sqrt(3))
View SolutionIf (5,12)and(24,7) are the foci of a hyperbola passing through the origin, then e=√38612 (b) e=√38613 LR=1216 (d) LR=1213
View SolutionThe foci of the hyperbola 3(y−1)2−4(x−2)2=12 are (0,√7) b. (−2,1−√7) c. 2,1−√7 d. (0)−√7
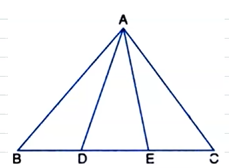
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
View SolutionLet R be a relation on N×N defined by (a,b) R(c,d)⇔a+d=b+c for all (a,b),(c,d)∈N×N show that: (i) (a,b)R (a,b) for all (a,b)∈N×N (ii) (a,b)R(c,d)⇒(c,d)R(a,b)for all (a,b), (c,d)∈N×N (iii) (a,b)R (c,d)and (c,d)R(e,f)⇒(a,b)R(e,f) for all (a,b), (c,d), (e,f)∈N×N
View Solution√24÷0.5+1+√18÷0.6+6=? (a) 19 (b) 13 (c) 12 (d) 15
View Solutionln(3√3)−ln(2+√3) equals (where lnx=logex)
View Solutionlog121(√14641121)= ____
View Solutionb 3 P, c 6 R, d 12 T, e 24 V, ?
View SolutionIf (5,12) and (24,7) are the foci of a hyperbola passing through the origin , then the eccentricity of the hyperbola is :
View SolutionIf (5,12), (24,7) are the foci of the hyperbola passing through origin, then its eccentricity is
View Solution
