Given the sum of the perimeters of a square and a circle, show that the sum of their areas is least when one side of the square is equal to diameter of the circle.
Let side of square be x, then radius of circle be y.
Sum of perimeters =S=4x+2πy
Sum of areas =A=x2+πy2
⇒A=x2+14π(S−4x)2
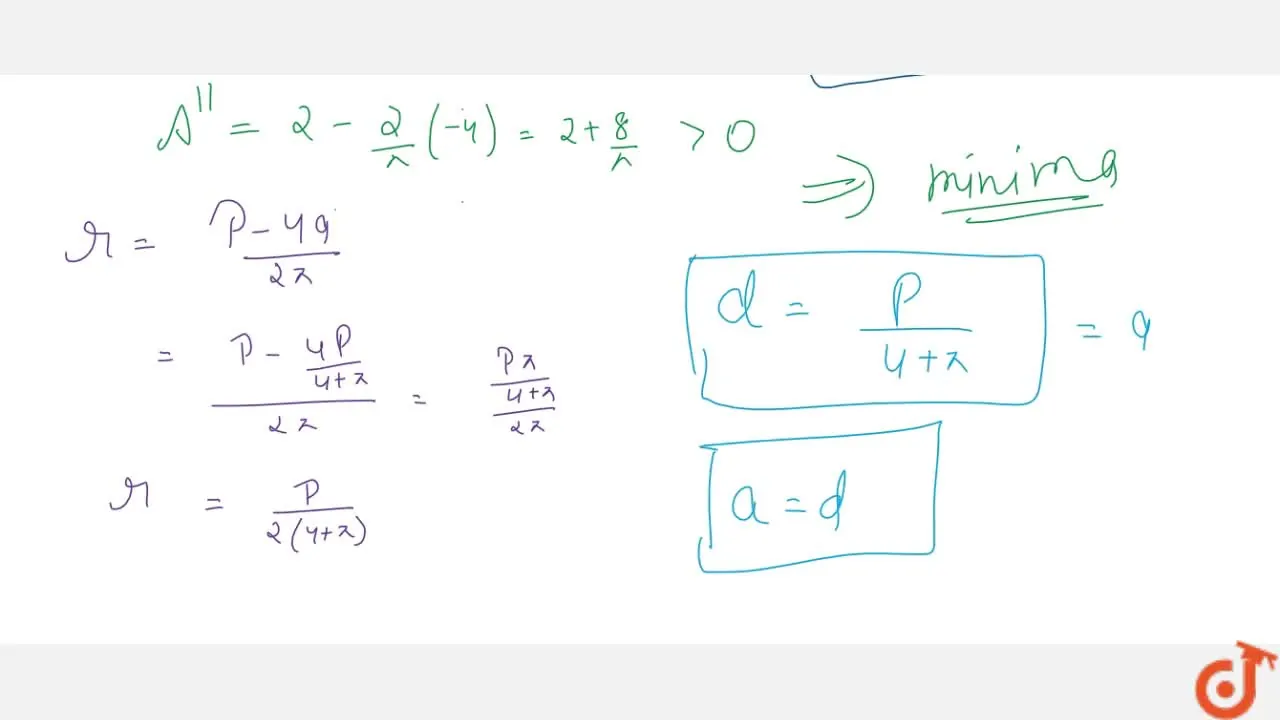
dAdx=2x−2π(S−4x)
Put dAdx=0
Thus 2x−2π(S−4x)=0
⇒x=S4+π
And d2Adx2=2+8π>0
Thus, A is minimum when x=S4+π and y=12π(S−4x)=12π(S−4Sπ+4)=S2(π+4)
We can clearly see that x=2y
⇒Side of square is equal to the diameter of the circle.
Hence Proved.
Related Playlists
Similar Questions
The sum of perimeter of a square and circumference of a circle is given. Prove that the sum of their areas will be minimum when the side of square is equal to the diameter of the circle.
View SolutionThe sum of the perimeters of a circle and a square is k , where k is some constant. Prove that the sum of their areas is least when the side of the square is double the radius of the circle.
View SolutionThe sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
View SolutionThe sum of the surface areas of a sphere and a cube is given. Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
View SolutionThe areas of a square and a circle are equal. The radius of the circle is r and the side of the square is S.Find the circumference of the circle in terms of S.
View SolutionThe areas of a square and a circle are equal. The radius of the circle is r and the side of the square is S.Find the circumference of the circle in terms of S.
View SolutionIf the perimeter of a circle is equal to that of a square, then the ratio of their areas is
View SolutionThe sum of the areas of two squares is 157m2 . If the sum of their perimeters is 68 m , find the sides of the two squares .
View SolutionThe perimeter of a square and circle is same. If the area of square is 484m2 then find the area of circle
View SolutionThe area of a square is 16π of the area of a circle. The ratio of the sides of the square to the diameter of the circle is
View Solution