Find the middle point of the chord of the circle x2+y2=25 intercepted on the line x−2y=2
The correct Answer is:(2/5,−4/5)
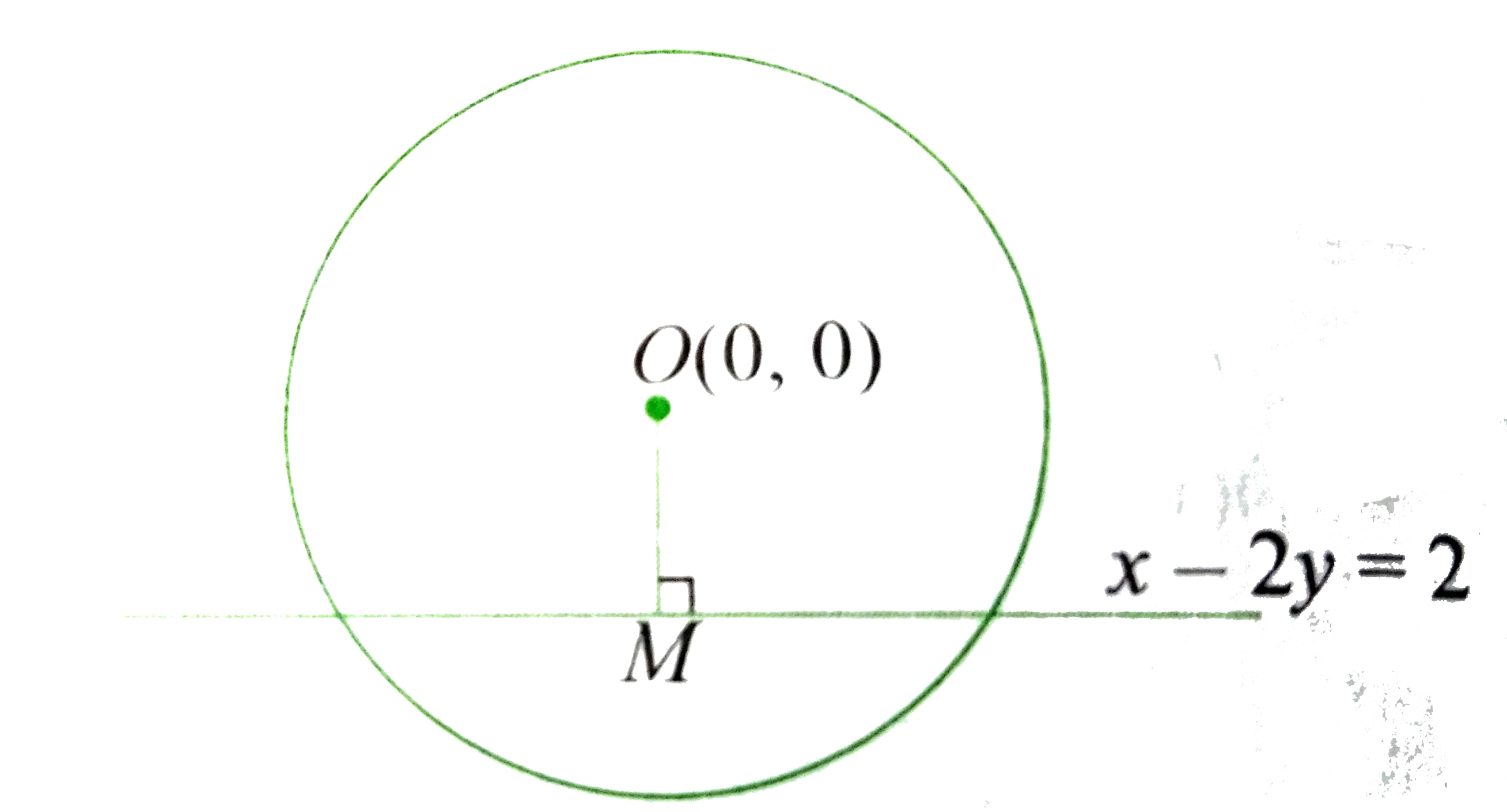
Let the middle point of chord be M(h,k) .
So, equation of OM is 2x+y=0.
Solving this line with chord x−2y=2, we get point M as (2/5,−4/5).
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.19
Explore 1 Video
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.20
Explore 1 Video
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.17
Explore 2 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
Knowledge Check
Find the length of the chord intercepted by the circle x2+y2−8x−6y=0 on the line x−7y−8=0.
A5B√2C5√2D6
Find the coordinates of the middle point of the chord which the circle x2+y2+4x−2y−3=0 cuts-off the line x-y+2=0.
View SolutionFind the length of the chord intercepted by the circle x2+y2=25 on the line 2x -y + 5= 0
View SolutionFind the mid point of the chord intercepted by the circle x2+y2−2x−10y+1=0 on the line x−2y+7=0
View SolutionFind the middle point of the chord intercepted on the line 2x-y+3 =0 by the ellipse x210+y26=1
View SolutionFind the length of the chord cut-off by y=2x+1 from the circle x2+y2=2
View SolutionFind the equation of that chord of the circle x2+y2=15, which is bisected at the point (3,2)
View SolutionThe equation of the locus of the middle point of a chord of the circle x2+y2=2(x+y) such that the pair of lines joining the origin to the point of intersection of the chord and the circle are equally inclined to the x-axis is x+y=2 (b) x−y=2 2x−y=1 (d) none of these
View Solution

