Find the area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣,andyl=2, which lies to the right of the line x=1.Solution in Bengali
The given curves are
y=x2 (1)
y=∣∣2−x2∣∣ (2)
The graphs of these curve are as follows :
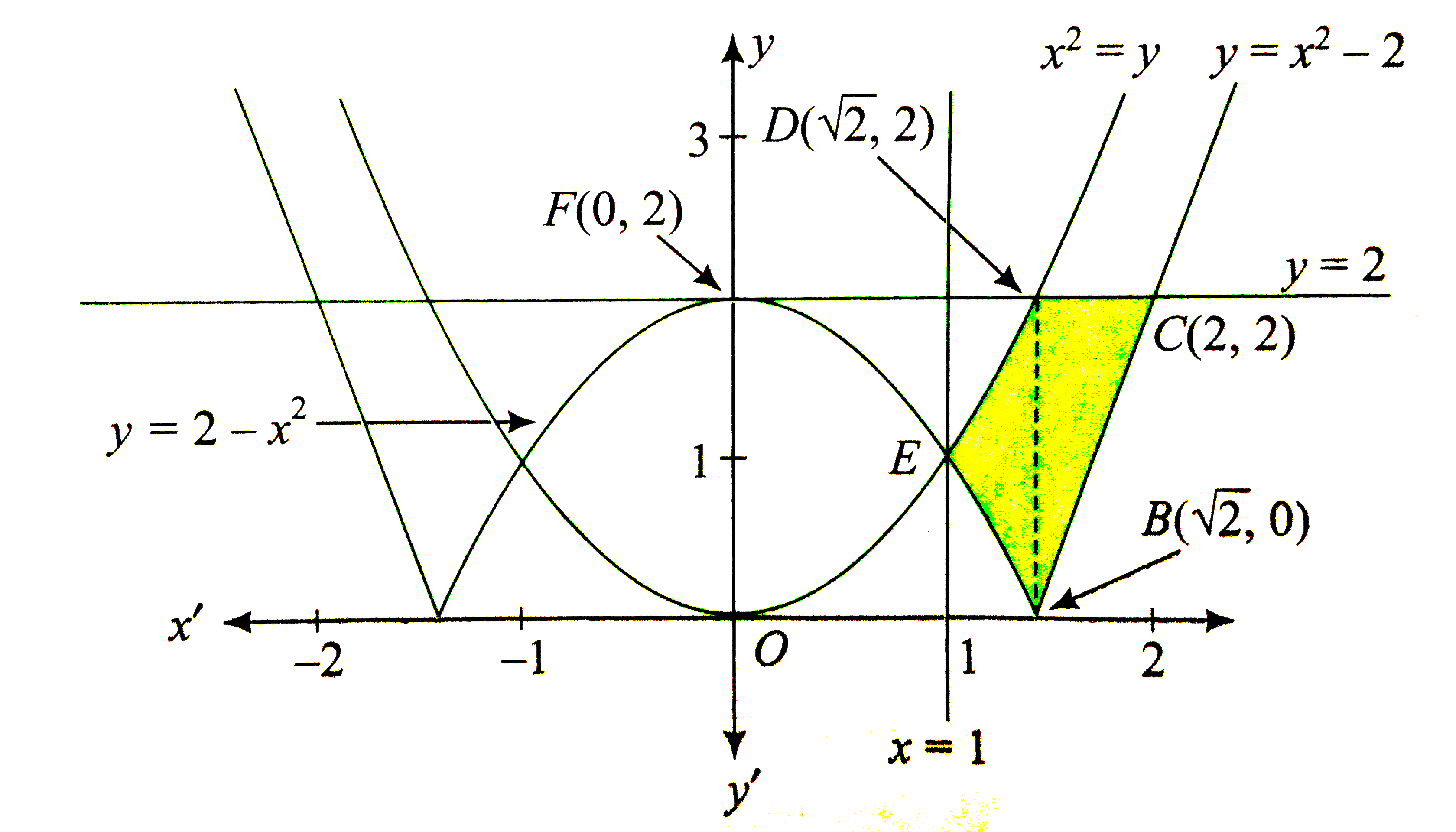
∴ Required area =BCDEB
=∫√21[x2−(2−x2)]dx+∫2√2[2−(x2−2)]dx
=∫√21(2x2−2)dx+∫2√2(4−x2)dx
=[2x33−2x]√21+[4x−x33]2√2
=(4√23−2√2−23+2)+(8−83−4√2+2√23)
=(203−4√2) sq. units.
Topper's Solved these Questions
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Concept Application Exercise 9.1
Explore 9 Videos
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Concept Application Exercise 9.2
Explore 14 Videos
- AREABook:CENGAGE PUBLICATIONChapter:AREAExercise:Comprehension Type
Explore 2 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGE PUBLICATIONChapter:APPLICATIONS OF DERIVATIVESExercise:Subjective Type
Explore 2 Videos
- BINOMIAL THEOREMBook:CENGAGE PUBLICATIONChapter:BINOMIAL THEOREMExercise:Comprehension
Explore 11 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionIn the following figure, the graphs of two functions y = f(x) and y = sin x are givne. They intersect at origin, A(a,f(a)),B(π,0)andC(2π,0).Ai(i=1,2,3) is the area bounded by the curves as shown in the figure, respectively, for x∈(0,a),x∈(a,π),x∈(π,2π).
If A1=1+(a−1)cosa−sin a, then

The function f(x) is
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionSketch the curves and identify the region bounded by the curves x=12,x=2,y=logxany=2x. Find the area of this region.
View SolutionArea of the region bounded by the curve y=x^(2),y=|2-x^(2)| and y=2, which liesto the right of the line x=1, is equal to
View SolutionThe area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣ and y=2 which lies to the right of the line x=1, is
View SolutionFind the area of the region bounded by the curve (y−1)2=4(x+1) and the line y= x-1
View Solutionवक्र y=x2 तथा रेखा x=1,x=2 एवं X-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View SolutionSketch the curves and identity the region bounded by x=12,x=2,y=lnx,andy=2x. Find the area of this region.
View SolutionThe area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣ and y=2 which lies to the right of the line x=1, is
View SolutionFind the area of the region bounded by the curves y=x2+2,y=x,x=0,andx=3.
View SolutionSketch the region bounded by the curves y=x2andy=21+x2 . Find the area.
View SolutionFind the area of the region bounded by the curves y=x2,y=∣∣2−x2∣∣,andyl=2, which lies to the right of the line x=1.
View SolutionFind the area bounded by the curve y2=4a2(x−1) and the lines x=1andy=4a.
View Solution

