Find the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.Solution in Bengali
The given curve is y=tanx (1)
When x=π/4,y=1
i.e., co-ordinates of P are (π/4,1)
∴ equation of tangent at P is y−1=(sec2π4)(x−π/4)
or y=2x+1−π/2
The graphs of (1) and (2) are as shown in the figure.
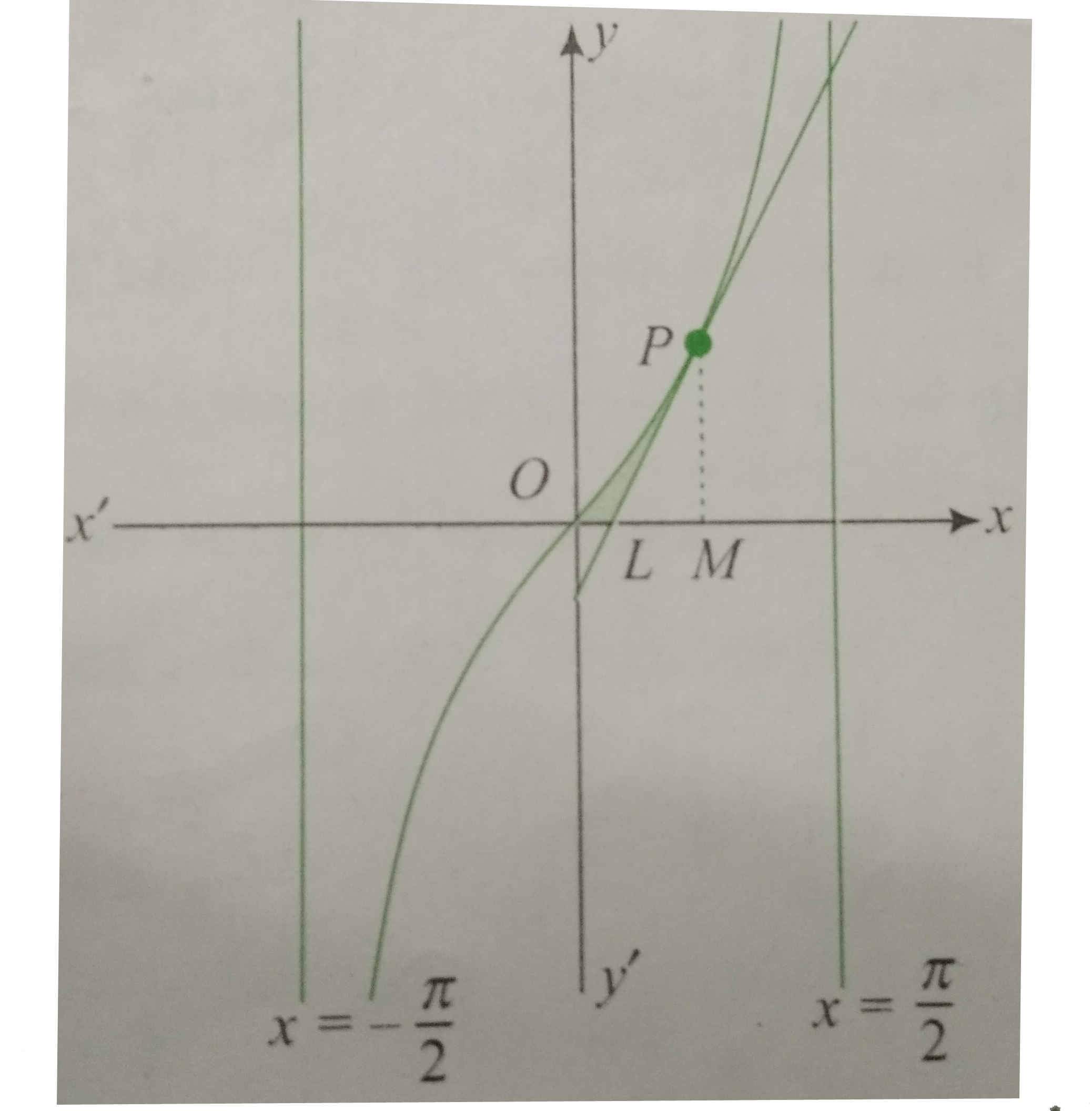
Tangent (2) meets x-axis at L(π−24,0)
Now, Required area =Shaded area
=Area OPMO−Ar(ΔPLM)
=∫π/40tanxdx−12(OM−OL)PM
=[logsecx]π/40−12×{π2−π−24}×1
=(1)/(2)[ log 2 -(1)/(2)]sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.2
14 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Comprehension Type
2 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionIn the following figure, the graphs of two functions y = f(x) and y = sin x are givne. They intersect at origin, A(a,f(a)),B(π,0)andC(2π,0).Ai(i=1,2,3) is the area bounded by the curves as shown in the figure, respectively, for x∈(0,a),x∈(a,π),x∈(π,2π).
If A1=1+(a−1)cosa−sin a, then

The function f(x) is
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionFind the area of the region bounded by the curve C:y=tan x, tangent drawn to C at x=(pi)/(4), and the x -axis.
View SolutionThe area of the region bounded by the curve y=tan x, tangent drawn to the curve at x=(pi)/(4) and the x -axis is
View SolutionFind the area of that region bounded by the curve y=cosx, X-axis, x=0 and x=π.
View Solutionवक्र C:y=tanx,x=π4 पर C से स्पर्श रेखा तथा x-अक्ष से सीमाबद्ध क्षेत्र का क्षेत्रफल-
View Solutionवक्र C:ytanx,x=π4 पर C से स्पर्श रेखा तथा x अक्ष से सीमाबद्ध क्षेत्र का क्षेत्रफल-
View SolutionFind the area of the region bounded by the curve y=sinx, the lines x=−π2,x=π2 and X- axis.
View SolutionFind the area of the region bounded by curve y=25x+16 and the curve y=b.5x+4, whose tangent at the point x=1 make an angle tan−1 (40 In 5) with the X-axis.
View SolutionThe area of the region (in square units) above the x - axis bounded by the curve y=tanx,0≤x≤π2 and the tangent to the curve at x=π4 is
View SolutionThe area of the region bounded by the curve y=tanx tangent drawn to the curve at x=π/4 and the x-axis is
View SolutionThe area of the region bounded by the curve y=tanx tangent drawn to the curve at x=π/4 and the x-axis is
View SolutionFind the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.
View Solution
