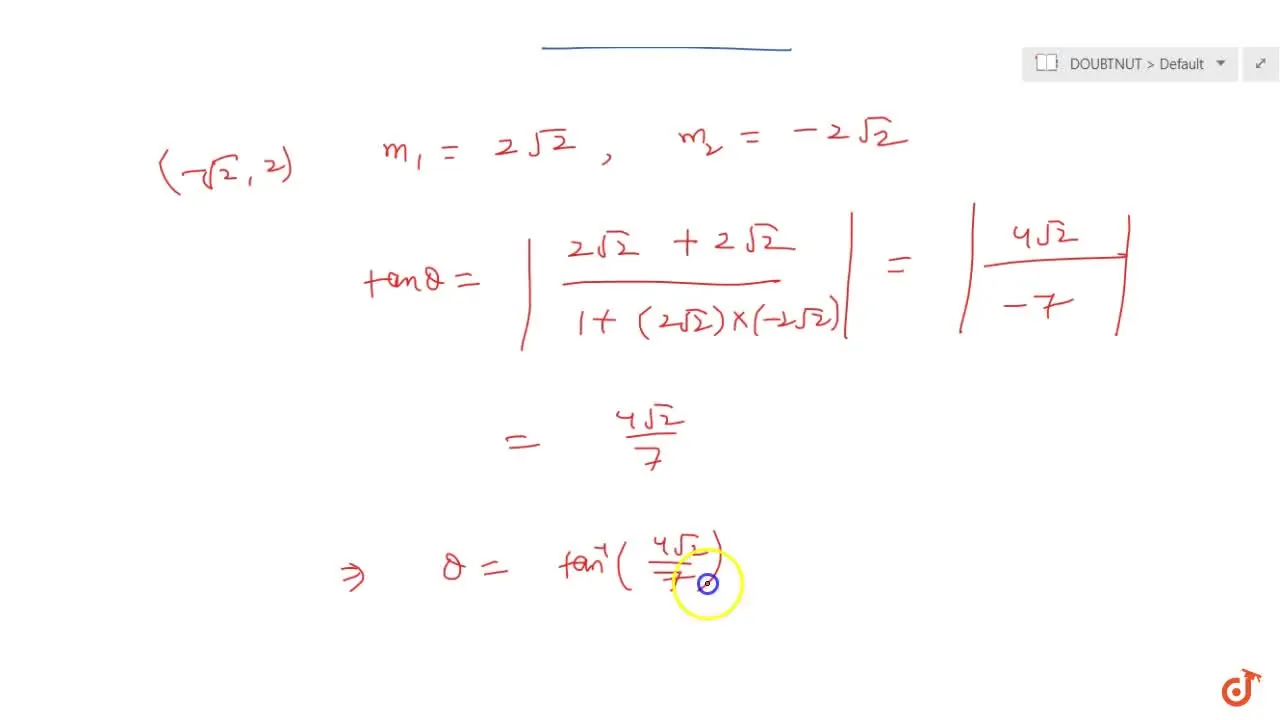Find the angle of intersection of the curves y=4−x2 and y=x2
A
θ=tan−1(4√27)
B
θ=tan−1(√27)
C
θ=tan−1(4√2)
D
θ=tan−1(√2)
Video Solution
Text Solution
The correct Answer is:A
We have , y=4−x2…………..(i)
and y=x2……………….(ii)
⇒dydx=−2x
and dydx=2x
⇒m1=−2x and m2=2x
From Eqs. ( i ) and ( ii ) ,
x2=4−x2
⇒2x2=4
⇒x2=2
∴x=±√2
∴y=x2=(±√2)2=2
So , the points of intersection are (√2,2) and (−√2,2).
And for point (√2,2)
m1=−2x=−2√2 , m2=2x=2√2
⇒tanθ=∣∣∣m1−m21+m1m2∣∣∣=∣∣∣−2√2−2√21−2√2.2√2∣∣∣=∣∣∣−4√2−7∣∣∣
θ=tan−(4√27)
And for point(−√2,2).
m1=−(2x).(−√2)=2√2
and m2=2x=−2√2
tanθ=∣∣∣m1−m21+m1m2∣∣∣=∣∣∣+2√2+2√21−2√2.2√2∣∣∣=∣∣∣4√2−7∣∣∣
θ=tan−(4√27)
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Find angle of intersection of the curves y=4−x2 and y=x2.
View SolutionFind the angle of intersection of the curves y=x2andy=4−x2.
View SolutionAngle of intersection of the curves y=4−x2 and y=x2 is
View SolutionFind the angle of intersection of the curves y2=xandx2=y
View SolutionFind the angle of intersection of the curves y2=4ax and x2=4by.
View SolutionFind the angle of intersection of the curves y2=4ax and x2=4by
View SolutionFind the angle of intersection of the curves xy=a2andx2+y2=2a2
View SolutionFind the angle of intersection of the curves :
(i) y2=4xandx2=4yView SolutionFind the angle of intersection of curves y=x3 and 6y=7−x2 at point (1,1)
View Solutionma bb, 1, m.Find the angle of intersection of the curve x2=32y and y2=4x at point (16,8).
View Solution