Draw the graph of y=3x−x31−3x2 and hence the graph of y=tan−1.3x−x31−3x2.
Text Solution
We have y=f(x)=3x−x31−3x2, which is an odd function.
Domain of the function is R−{±1√3}
1. y-intercept
f(0)=0
So the graph cuts the y-axis at (0,0).
2. x-intercept (zeros)
Put y=0 or 3x−x3=0∴x=0,±√3
So the graph meets the x-axis at (0,0) and (±√3,0).
3. Asymptotes
Vertical asymptotes
Clearly , the graph has vertical asymptote x=±1√3, where the denominator becomes zero.
Horizontal asymptotes
Clearly, the graph has no horizontal asymptote as the degree of the numerator is higher than the degree of the numerator is higher than the degree of the denominator.
Oblique asymptotes ltbr> y=x3−3x3x2−1=13x−−89x3x2−1
Hence the oblique asymptote is y=13x.
Thus, important points ans lines are as shown in the following figure.
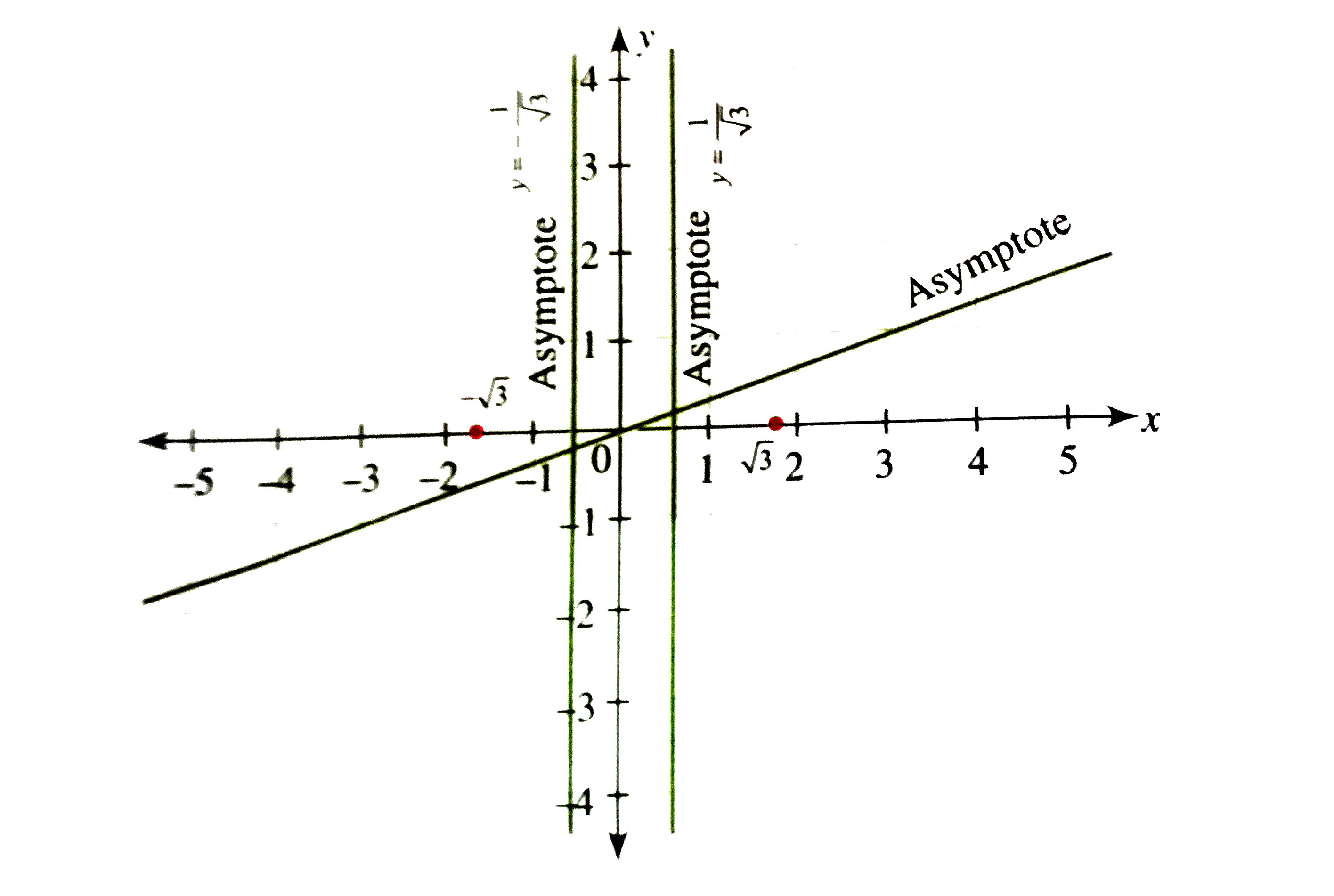
4. Monotinicity/Extremum
f'(x)=(3−3x2)(1−3x2)+6x(3x−x3)(1−3x2)2
=3(x2+1)2(1−3x2)2>0
Hence the function is increasing throughout.
limx→−1−√33x−x31−3x2=∞ and limx→−1+√33x−x31−3x2=−∞
f(x) approaches asymptote y=x/3 as x→−∞.
Thus, in (−∞,−1√3), f(x) increases from '−∞' to '∞' intersecting the x-axis at (−√3,0)
limx→−1+√33x−x31−3x2=−∞ and limx→√3−3x−x31−3x2=∞
Thus, in (−1√3,1√3), f(x) increases from '−∞' to '∞' intersecting the x-axis at (0,0).
limx→√3+3x−x31−3x2=−∞ and limx→∞3x−x31−3x2=∞
Thus, in (1√3,∞),f(x) increases from '−∞' to '∞' intersecting the x-axis at (√3,0).
f(x) approaches asymptote y=x/3 as x→∞.
From the above discussion, the graph of y=f(x) can be drawn as follows.
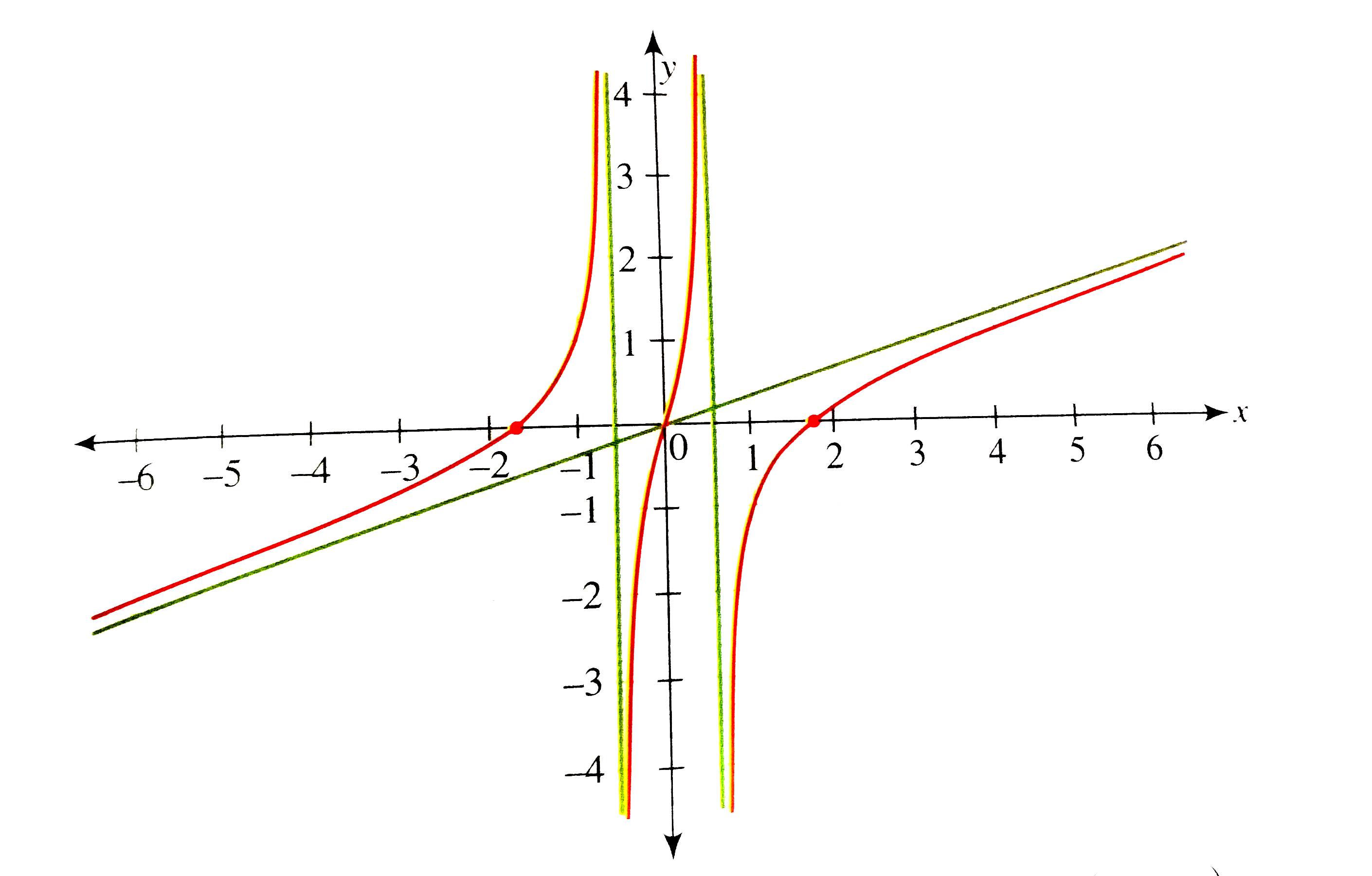
Now in each of the intervals (−∞,−1√3),(−1√3,1√3),(1√3,∞),f(x) takes values (−∞,∞).
So in each of the intervals, tan−1.3x−x31−3x2 takes values (−π2,π2).
So the graph of g(x)=tan−1.3x−x31−3x2 can be drawn as follows.
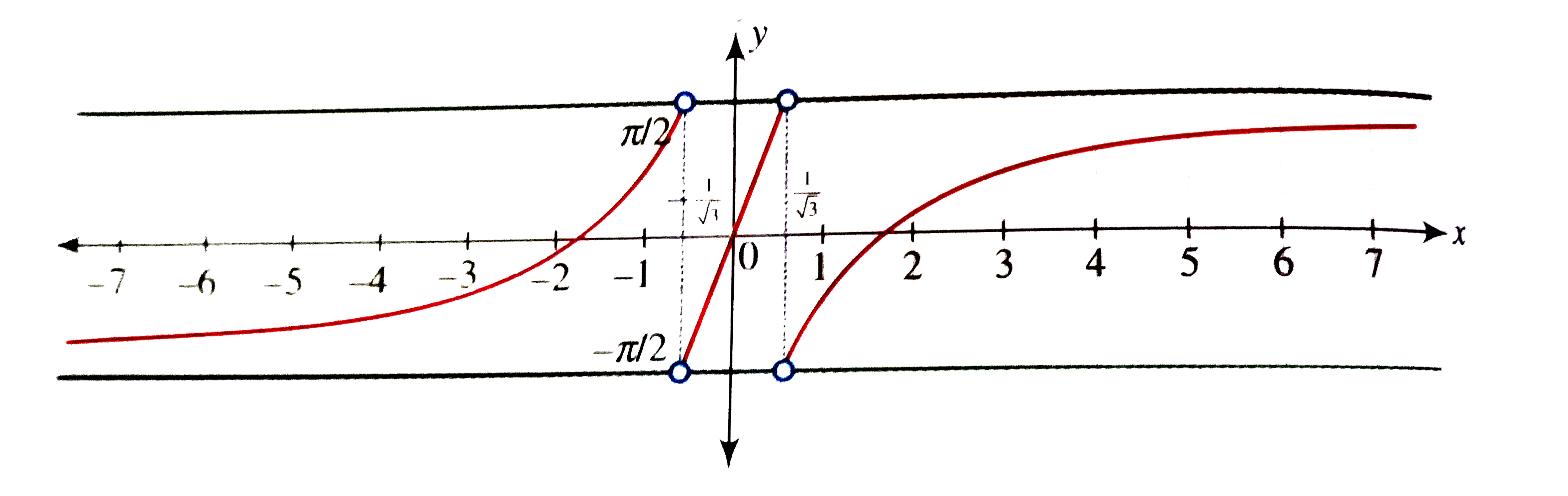
Here y=±π2 are asymptotes.
|
Updated on:21/07/2023
Related Playlists
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise22videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=tan−1(3x−x31−3x2).
View SolutionDraw the graph of y=tan−1(3x−x31−3x2).
View SolutionSketch the graph for y=tan−1(3x−x31−3x2)
View SolutionDraw the graph of y=x33(x+1).
View SolutionDraw the graph of y=x33(x+1).
View SolutionDraw the graph of y = 3x +1.
View SolutionDraw the graph of y=tan(3x).
View SolutionDraw the graph of y=tan(3x).
View SolutionDraw the graph of y=x−1x2 and hence the graph of y=|x−1|x2.
View SolutionDraw the graph of y=x−1x2 and hence the graph of y=|x−1|x2.
View Solution

