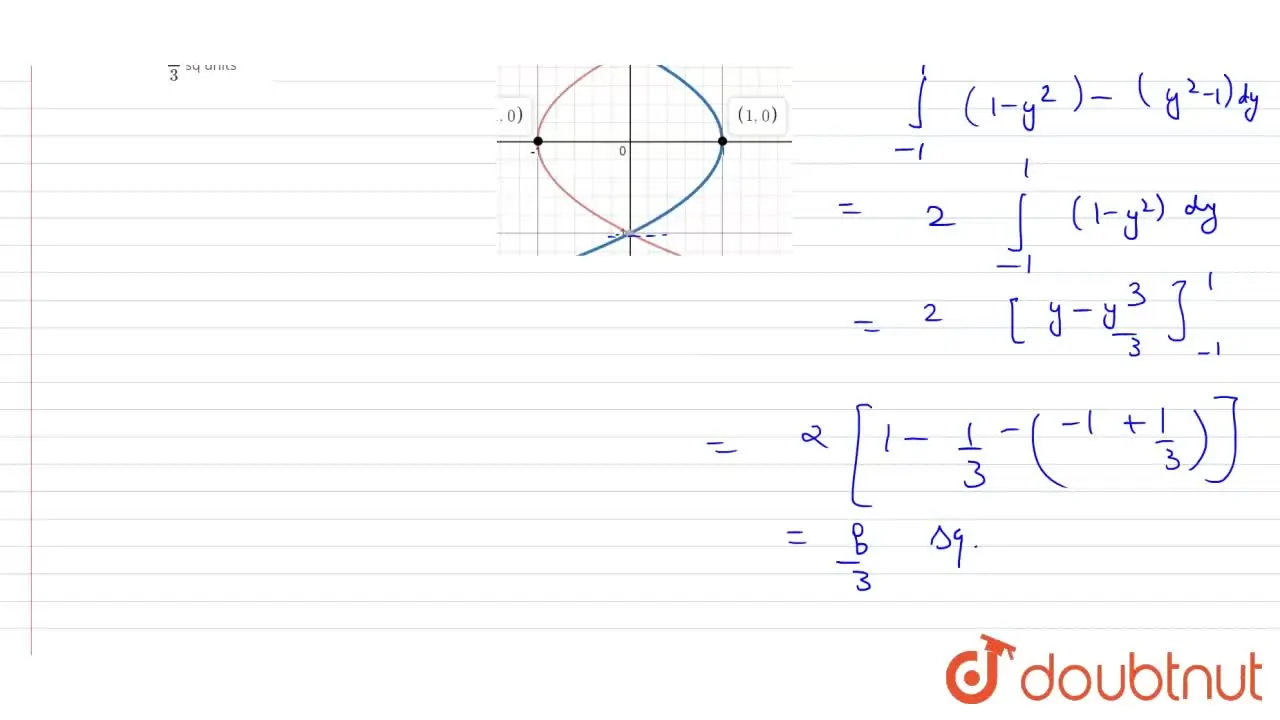
Determine the area enclosed by the two curves given by y2=x+1 and y2=−x+1
A
83 sq units
B
43 sq units
C
94 sq units
D
73 sq units
Video Solution
Text Solution
The correct Answer is:A
Given curves are
y2=x+1 ... (i)
y2=−x+1 ... (ii)
curve (i) is the parabola having axis y = 0and vertex (-1, 0).
Curve (ii) is the parabola having axis y = 0 and vertex (1, 0).
On solving Eq. (i) from Eq. (ii), we get 2x = 0 implies x = 0
From Eq. (i), x = 0 implies y=±1
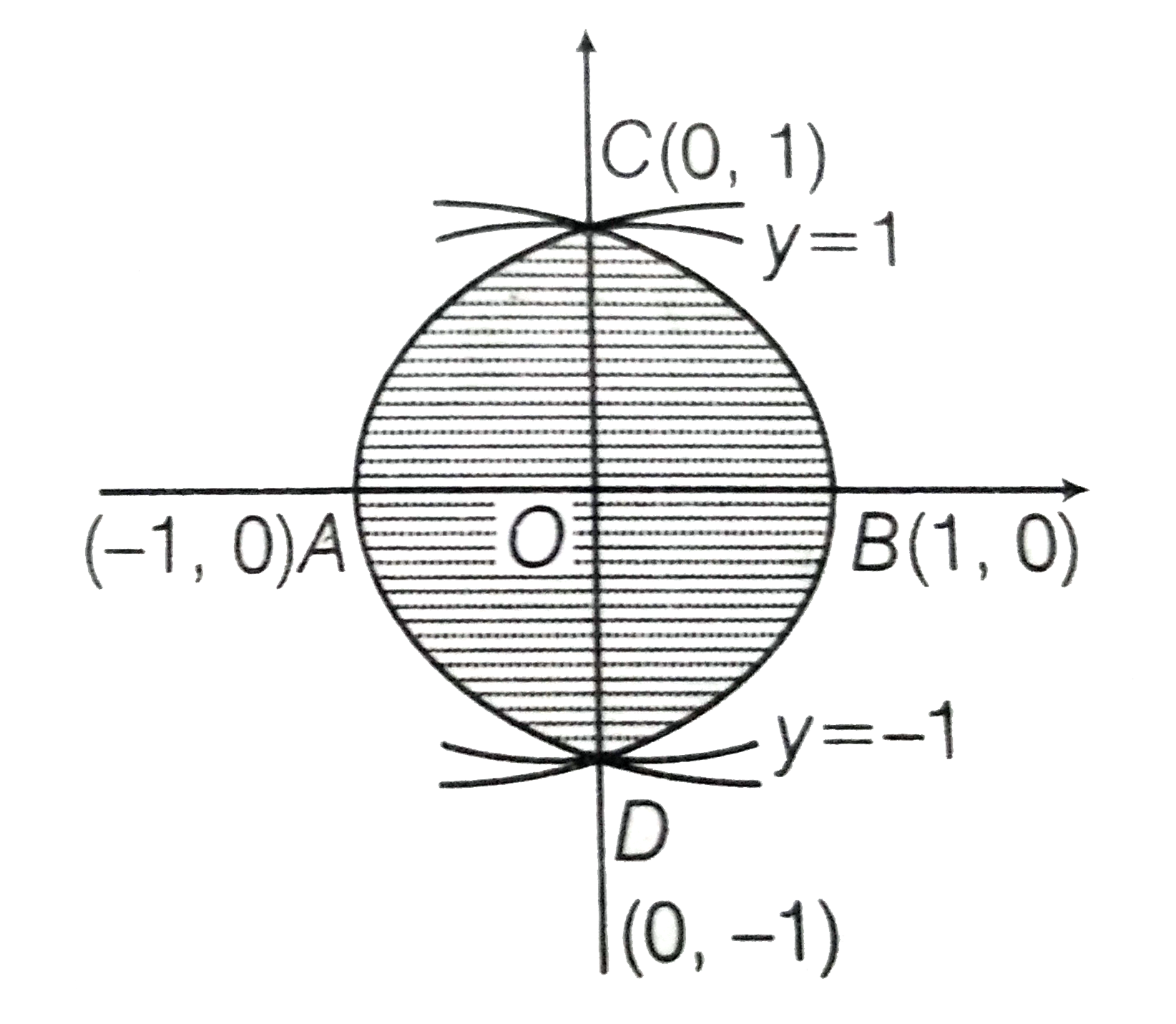
Required area
=∫1−1(x1−x2)dy
=∫1−1[(1−y2)−(y2−1)]dy=2∫1−1(1−y2)dy
=2[y−y33]1−1
=2[(1−13)−(−1+13)]=83 sq unit
|
Updated on:21/07/2023
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - Exercise 234videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner6videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER21videos
APPLICATIONS OF DERIVATIVES
Similar Questions
What is the area enclosed by the curve 2x2+y2=1 ?
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the area enclosed by the curves
max(|x|,|y|)=1View SolutionFind the area enclosed by the curves x2=y,y=x+2,andx−aξs.
View SolutionThe area enclosed by the curve y2=x4(1−x2) is
View SolutionFind the area enclosed by the curves
max(2|x|,2|y|)=1View SolutionWhat is the area enclosed by the curve 2x2+y2=1?
View SolutionCompute the area enclosed by the curve y2=(1−x2)3
View SolutionThe area enclosed by the curve y2+x4=x2 is
View SolutionCompute the area enclosed by the loop of the curve y2=x(x−1)2
View Solution