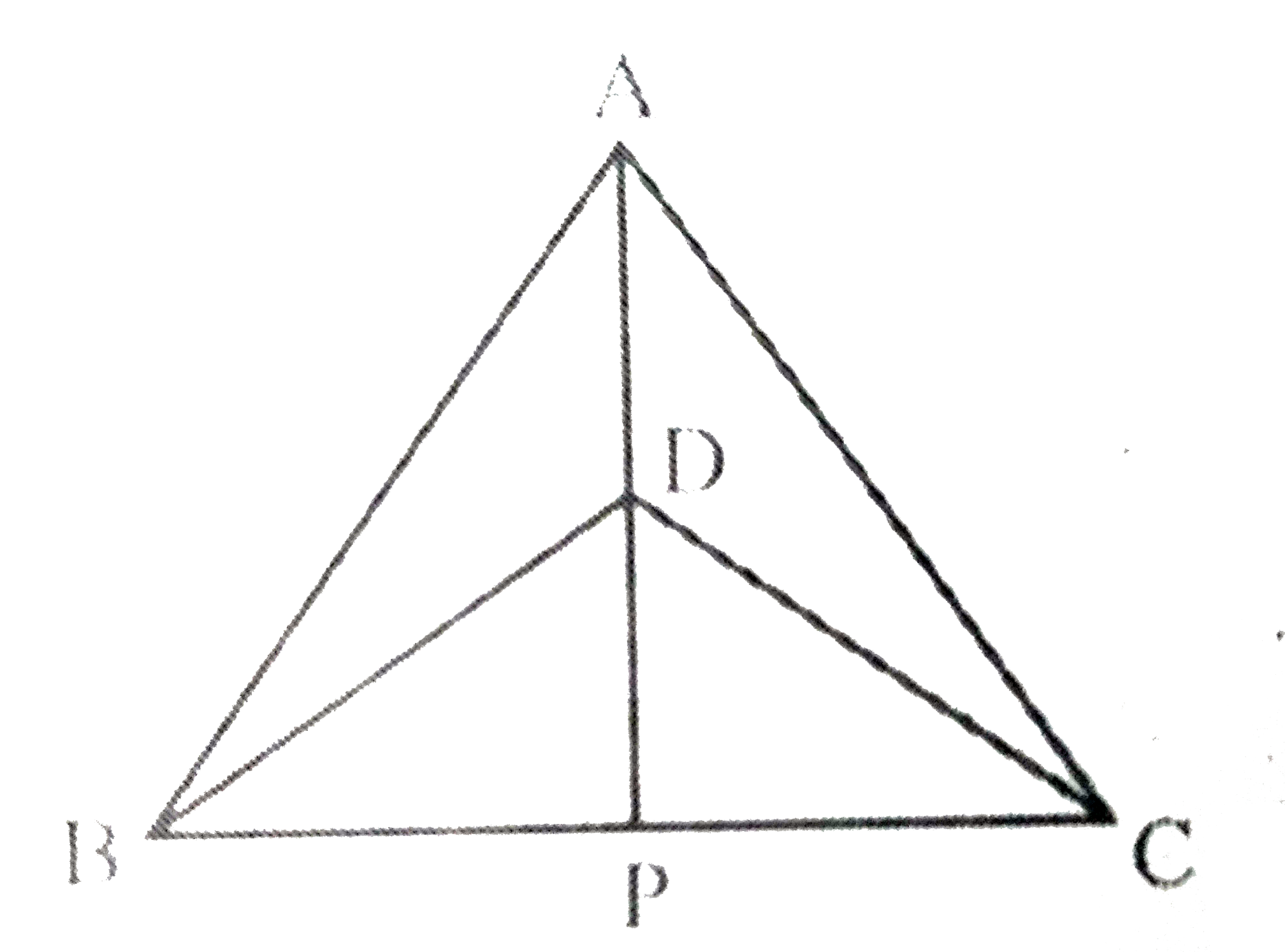
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
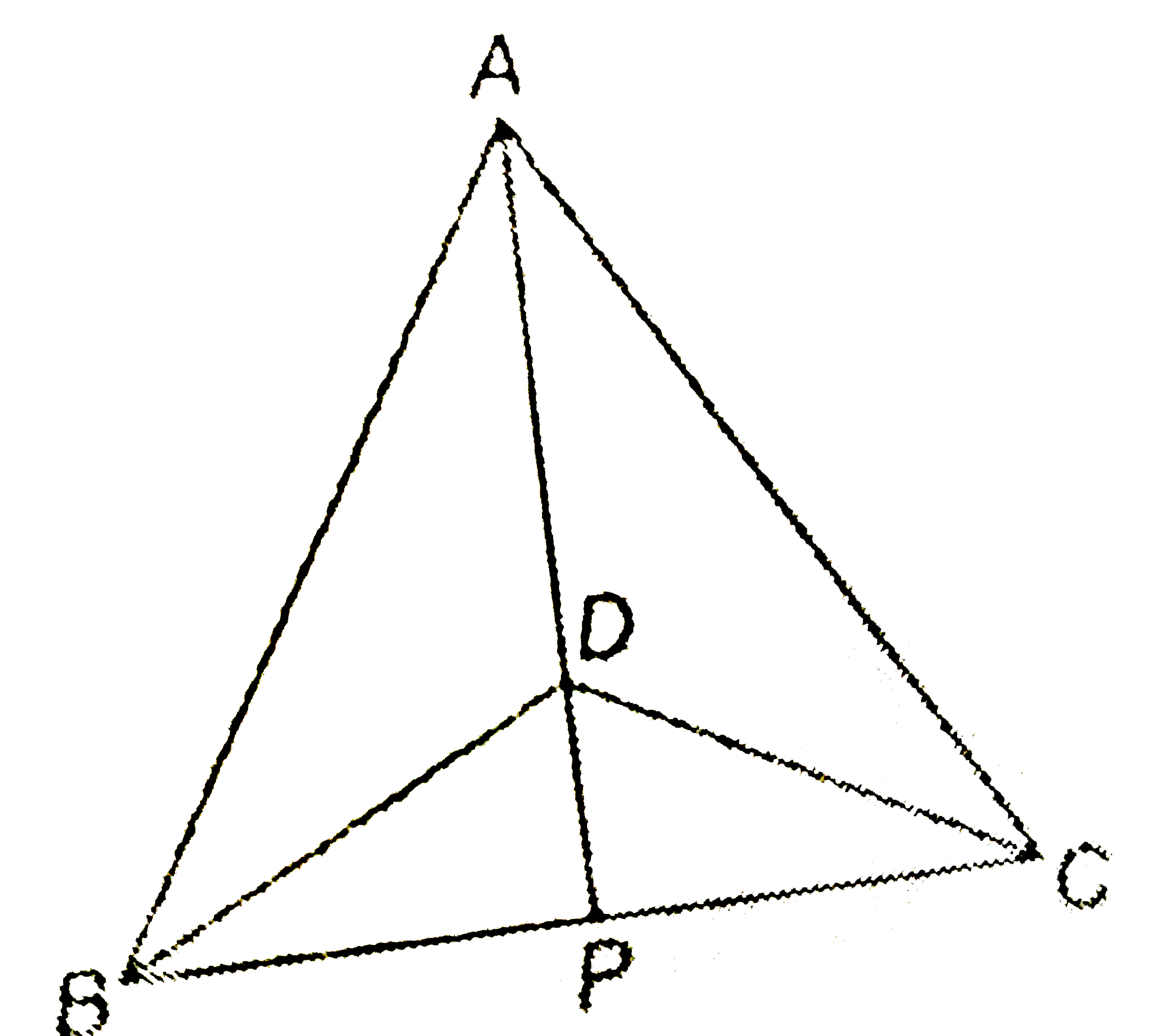
Given : ΔABC and ΔDBC are two isosceles triangles having common base BC, such that AB=AC and DB = DC.
To prove : (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
Proof : (i) In ΔABD and ΔACD, we have
AB=AC (given)
BD=CD (given)
and AD=AD (common)
∴ΔABD≅ΔACD (by SSS congruence axiom)
(ii) In ΔABP and ΔACP, we have
AB=AC (given)
∠1=∠2 (∵ΔABD≅ACD)
and AP=AP (common)
∴ΔABP≅ΔACP (by SAS congruence axiom)
(iii) ∠1=∠2(∵ΔABD≅ΔACD)
⇒ AP bisects ∠A
∠ADB=∠ADC(∵ΔABD≅ΔACD)
⇒ 180∘−∠ADB=180∘−∠ADC
⇒ ∠BDP=∠CDP (by linear pair axiom)
⇒ AP bisects ∠D.
(iv) BP=CP (∵ΔABP≅ΔACP)
and ∠3=∠4 ...(1)
But ∠3+∠4=180∘ (linear pair)
∴∠3+∠3=180∘ ⇒ ∠3=90∘ [from (1)]
⇒∠3=∠4=90∘
Hence, AP is the perpendicular bisector of BC.

Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Exercise 7a
Explore 35 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHANChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
ΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
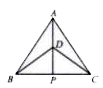
ΔABP≅ΔACP
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
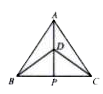
ΔABD≅ΔACD
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
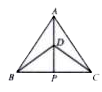
AP bisects ∠A as well as ∠D.
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
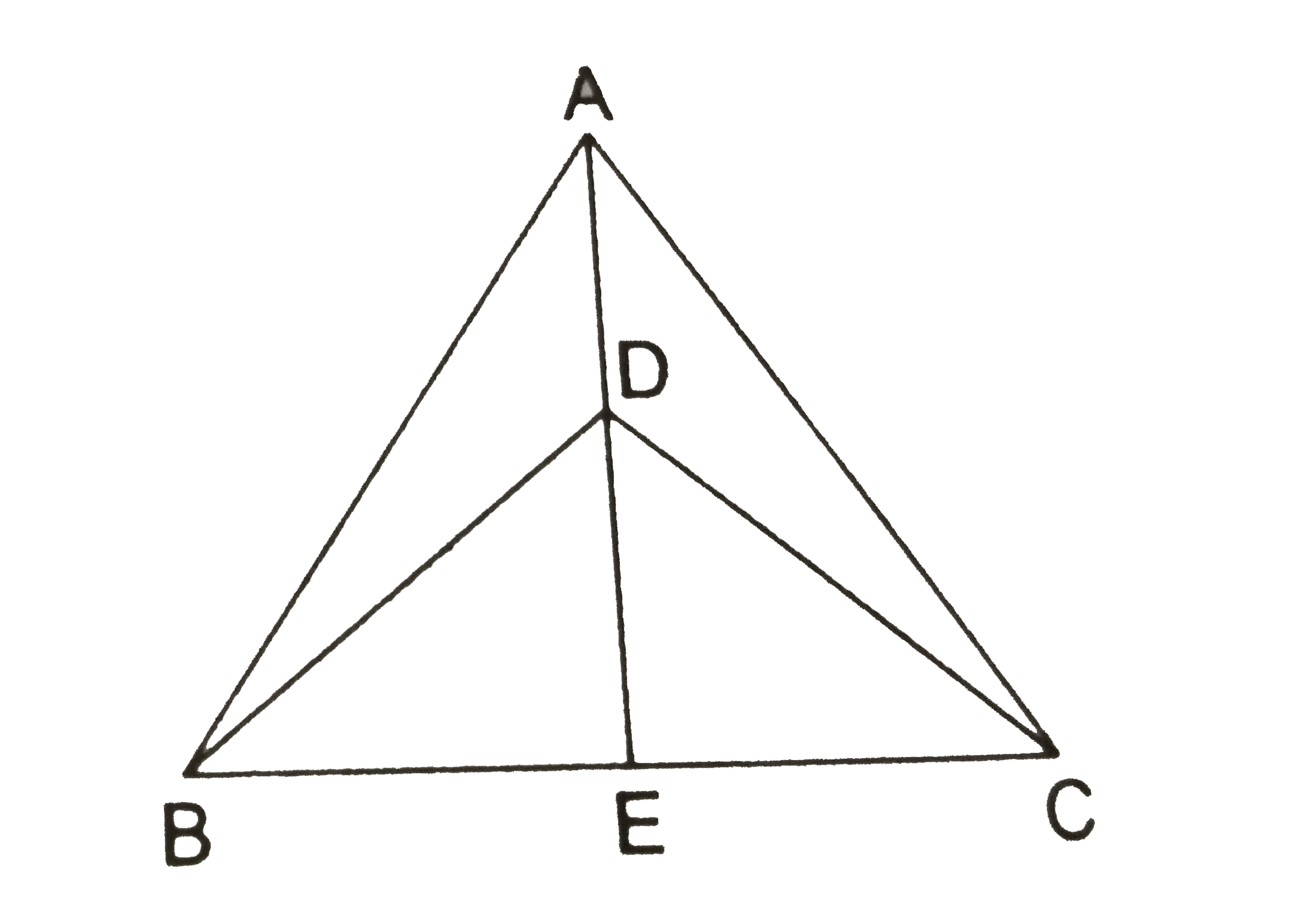
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that
(i) ΔABD≅ΔACD
(ii) ΔABE≅ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicualr bisector of BC.
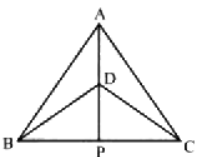
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D. (iv) AP is the perpendicular bisector of BC.
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD≅ACD (ii) ABP≅ACP AP bisects ∠A as well as ∠D AP is perpendicular bisector of BC.
View Solution

