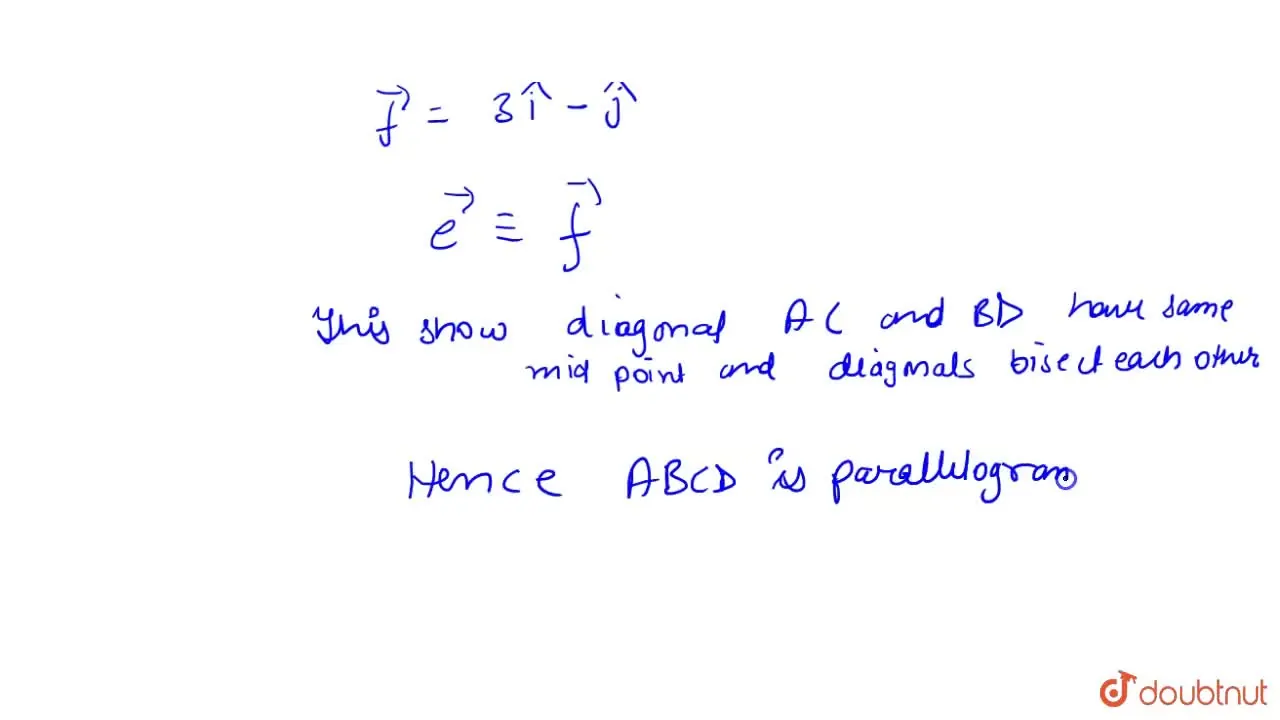By method, show that the quadrilateral with vertices A(1,2,-1), B(8,-3,-4), C(5,-1,1),D(-2,1,4) is a parallelogram.
Let be the position vectors of A,B,C,D respectively w.r.t the origin
Then ,
Let be midpoints of AC and respectively.
Then
From (a) and (2), we get, . . . .(2)
This show that the midpoints of diagonals AC and BD are same the diagonals AC and BD bisect each other.
Hence, the quadrilateral ABCD is a parallelogram.
Related Playlists
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VECTORSEXERCISE - Theory Questions4videos
VECTORS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VECTORSEXERCISE - Examples for Practics28videos
VECTORS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Choice Questions12videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the area of the quadrilateral with vertices A(1,2), B(2,2), C(3,3), D(5,3).
View SolutionFind the area of the quadrilateral whose vertices are A(1,1),B(3,4),C(5,−2) and D(4,−7)
View SolutionShow that A(1,−2),B(3,4),C(5,10),D(3,2) are the vertices of parallelogram.
View SolutionThe area of the quadrilateral ABCD where A(0,4,1), B(2,3,-1), C(4,5,0) and D(2,6,2), is equal to
View SolutionThe area of the quadrilateral ABCD where A(0,4,1),B(2,3,−1),c(4,5,0)andD(2,6,2) is to :
View SolutionBy vector method, show that the four points (7,2,−3),(6,1,4),(−3,−4,−1)and(−2,−3,−8) are the vertices of a parallelogram.
View SolutionShow that the coplanar points (−1,2,1),(1,−2,5),(4,−7,8)and(2,−3,4) are the vertices of a parallelogram.
View SolutionShow that points A(-1, 0) , B(-2,1) , C(1,3) and D(2,2) form a parallelogram .
View SolutionShow that the points A(1,2,3), B(-1,-2,-1), C(2,3,2), D(4,7,6) are the vertices of a parallelogram.
View SolutionFind the area of quadrilateral ABCD whose vertices are A(-3, -1), B(-2, -4), C(4, -1) and D(3, 4).
View Solution