At a point P on the ellipse x2a2+y2b2=1 tangents PQ is drawn. If the point Q be at a distance 1p from the point P, where 'p' is distance of the tangent from the origin, then the locus of the point Q is
A
x2a2+y2b2=1+1a2b2
B
x2a2−y2b2=1−1a2b2
C
x2a2+y2b2=1a2b2
D
x2a2−y2b2=1a2b2
Text Solution
The correct Answer is:A
Equation of the tangent at P is
x−acosθasinθ=y−bsinθ−bcosθ
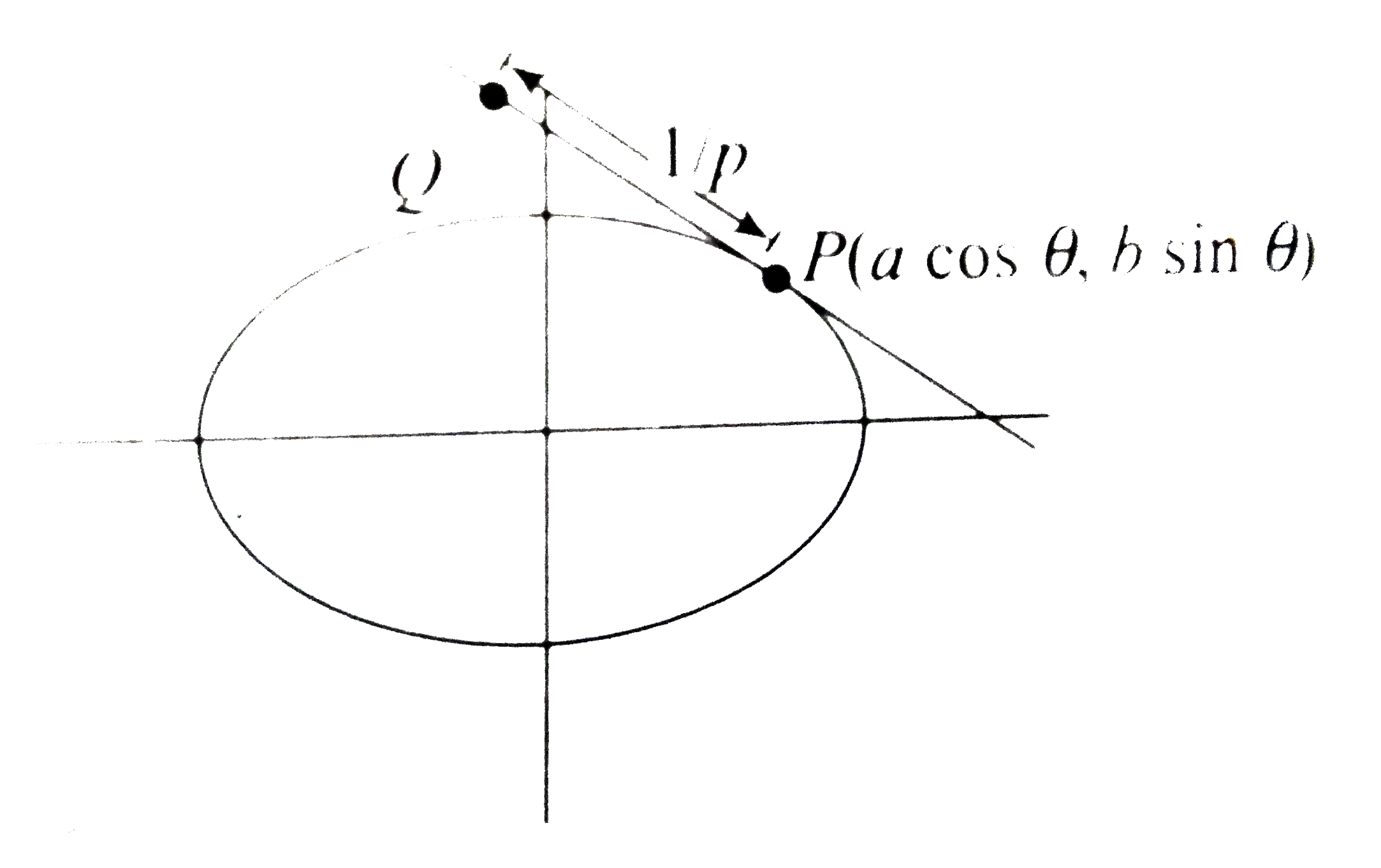
The distance of the tangent from the origin is
p=∣∣
∣∣ab√b2cos2θ+a2sin2θ∣∣
∣∣
⇒1p=√b2cos2θ+a2sin2θab
Now the coordinates of the point Q are given as follows
x−acosθ−asinθ√b2cos2θ+a2sin2θ=y−bsinθbcosθ√b2cos2θ+a2sin2θ=1p=√b2cos2θ+a2sin2θab
⇒x=acosθ−asinθab and y=bsinθbcosθab
⇒(xa)2+(yb)2=1+1a2b2 is the required locus.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The tangent at P on the hyperbola x2a2−y2b2=1 meets one of the asymptote in Q. Then the locus of the mid-point of PQ is
A3(x2a2−y2b2)=4Bx2a2−y2b2=2Cx2a2−y2b2=12D4(x2a2−y2b2)=3 - Question 2 - Select One
If P is the point (1,0) and Q is any point on the parabola y2=8x then the locus of mid - point of PQ is
AP1 lies on C2andQ1 lies on C1BPQ≥min{PP1,QQ1}Cpoint P0 on C1 such that P0Q0≤PQ for all pairs of points (P,Q) is (13,109)Dpoint Q0 on C2 such that P0Q0≤PQ for all pairs of points (P,Q) is (109,13) - Question 3 - Select One
Let P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
Ax2−2xy−8=0Bx2+4y+2=0Cy2+4x+2=0Dy2−4x+2=0
let P be the point (1,0) and Q be a point on the locus y2=8x. The locus of the midpoint of PQ is
View SolutionThe tangent at an arbitrary point R on the curve x2p2−y2q2=1 meets the line y=qpx at the point S, then the locus of mid-point of RS is
View SolutionFind the equation of the locus of a point P such that the distance of P from the origin is twice the distance of P from A(1,2).
View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :
View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :
View Solution
