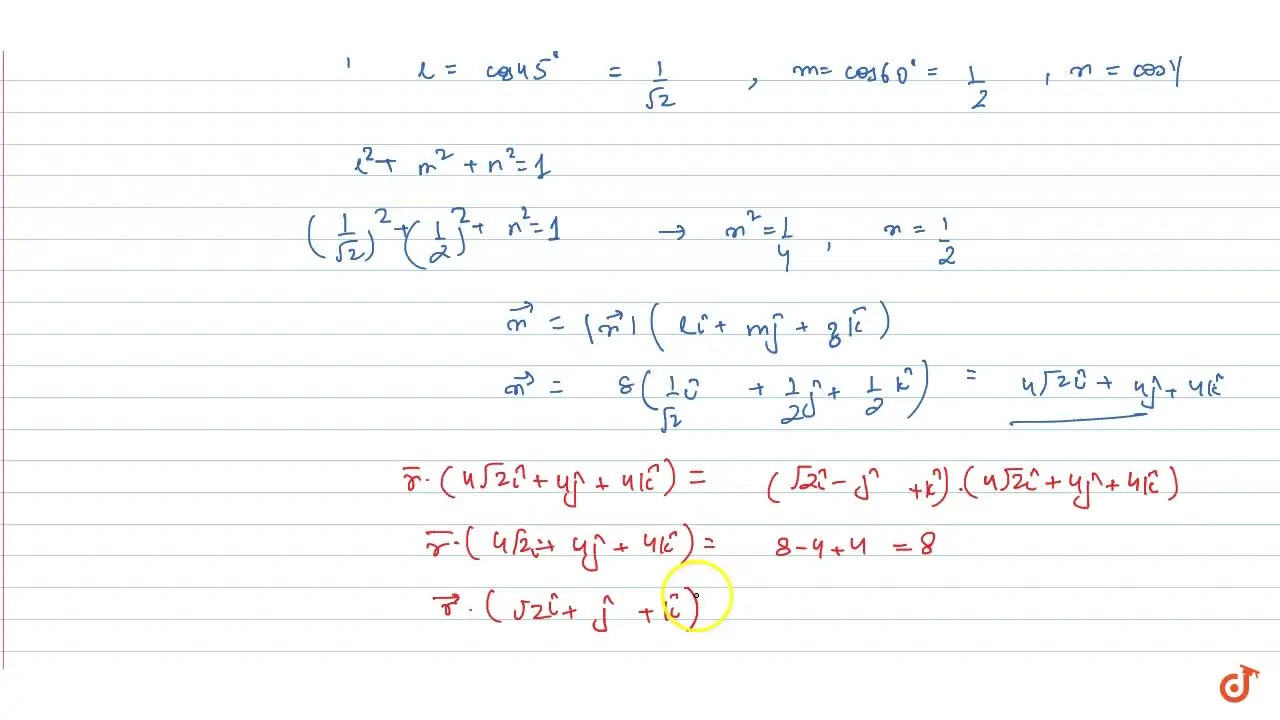A vector →n of magnitude 8 units is inclined to x-axis at 450 , y-axis at 600 and an acute angle with z-axis. If a plane passes through a point (√2,−1,1) and is normal to →n , find its equation in vector form.
Given,
l=cos(45)0=1√2,m≡cos(60)0=12,n=cosα
We know that,
=l2+m2+n2=1
=(cos(45)0)2+(cos(60)0)2+n2=1
=12+14+n2=1
=n=12
So,
→n=|n|(lˆi+mˆj+njatk)
=→n=8(1√2ˆi+14ˆj+12ˆk)
=→n=4sqr2ˆi+4ˆj+4ˆk
So, its vector equation is:
=r.n=a.n
=r.(4√2ˆi+4ˆj+4ˆk)=(√2ˆi−ˆj+ˆk).(4√2ˆi+4ˆj+4ˆk)
=r.(4√2ˆi+4ˆj+4ˆk)=8
=r(√2ˆi+ˆj+ˆk)=2
Related Playlists
Similar Questions
A vector →n of magnitude 8 units is inclined to x-axis at 450 , y-axis at 600 and an acute angle with z-axis. If a plane passes through a point (√2,−1,1) and is normal to →n , find its equation in vector form.
View SolutionA vector →n is inclined to x-axis at 45∘, to y-axis at 60∘ and at an angle to z-axis. If →n is a normal to the plane passing through the point (√2,−1,1), then the equation of plane is
View SolutionA vector →r is inclined to x-axis at 45∘ and y-axis at 60∘ if |→r|=8 units. Find →r.
View SolutionFind a vector →a of magnitude 5√2 making an angle π4 with x-axis , π2 with y-axis and an acute angle θ with z-axis
View SolutionFind a vector a of magnitudes 5√2 ,making an angle of π4 with X-axis ,π2 with Y-axis and an acute angle θ with Z-axis
View SolutionA vector →r is inclined to x-axis at 450 and y-axis at 600. If |→r|=8 units, find →r.
View SolutionFind a vector →a of magnitude 5√2 making an angle of π4 with x-axis, π2 with y-axis and an acute angle θ with z-axis.
View SolutionWrite a vector of magnitude 12 units which makes 450 angle with X-axis 600 angle with Y-axis and an obtuse angle with Z-axis.
View SolutionFind the vector and cartesian equations of the plane that passes through the point (0,1,−2) and normal to the vector ˆi+ˆj+ˆk.
View SolutionFind the equation of the line passing through the point (2, 2) and inclined to x-axis at 450.
View Solution