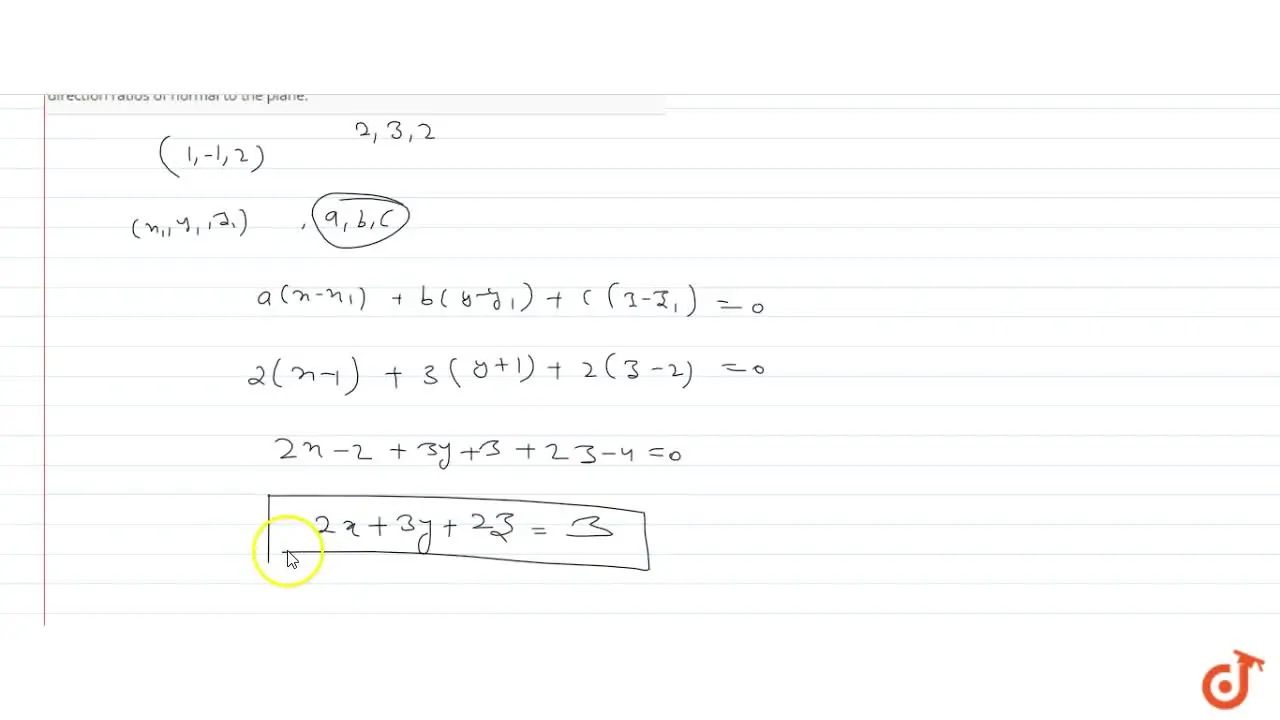Find the equation of the plane passing through the point (1,−1,2) having 2,3,2 as direction ratios of normal to the plane.
Given,
the plane has position vector a
ˆi−ˆj+2htk
and is normal to the vector n
=2ˆi+3ˆj+2ˆk
So, the vector equation of the plane is
=r.n=a.n
=r.(2ˆi+3ˆj+2ˆk)=(ˆi−ˆj+2ˆk).(2ˆi+3ˆj+2ˆk)
=r.(2ˆi+3ˆj+2ˆk)=3
Thus,
the cartesian equation of the plane is 2x+3y+2z=3
Related Playlists
Similar Questions
The eyation of plane passing through the point (1 ,1 ,2) having 2 ,3 ,2 as direction ratios of normal to the plance is
View SolutionThe equation of plance passing through the point (1 ,1 -2) having 2, 3, 2 as direction ratios of normal to the plance is
View SolutionThe equation of plance passing through the point (1,1−2) having 3, 2,3 as direction ratios of normal to the plance is
View SolutionFind the equation of the plane passing through the point (2,3,1) having (5,3,2) as the direction ratio is of the normal to the plane.
View SolutionFind the general equation of plane pasing through the point (1,2,−3).
View SolutionThe equation of the plane passing through the points (1,2,3), (-1,4,2) and (3,1,1) is
View SolutionThe equation of a plane passing through (0,1,-3) and having 1,2,4 as direction ratios of normal to the plane is
View Solutionfind the equation of the plane passing through points (2,1,0),(5,0,1) and (4,1,1).
View SolutionFind the equation of the plane passing through the points (2,1,2)and(1,3,−2) and parallel to the x-axis.
View SolutionThe equation of plane passing through the points (1,2,-3),(3,1,0) and (0,1,1) is
View Solution