A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.
1150
1350
1750
1950
The correct Answer is:A
let the event of lost card is diamond be A
let the event of both drawn card is diamond be B
P(A)=1352=14
P'(A)=1−14=34
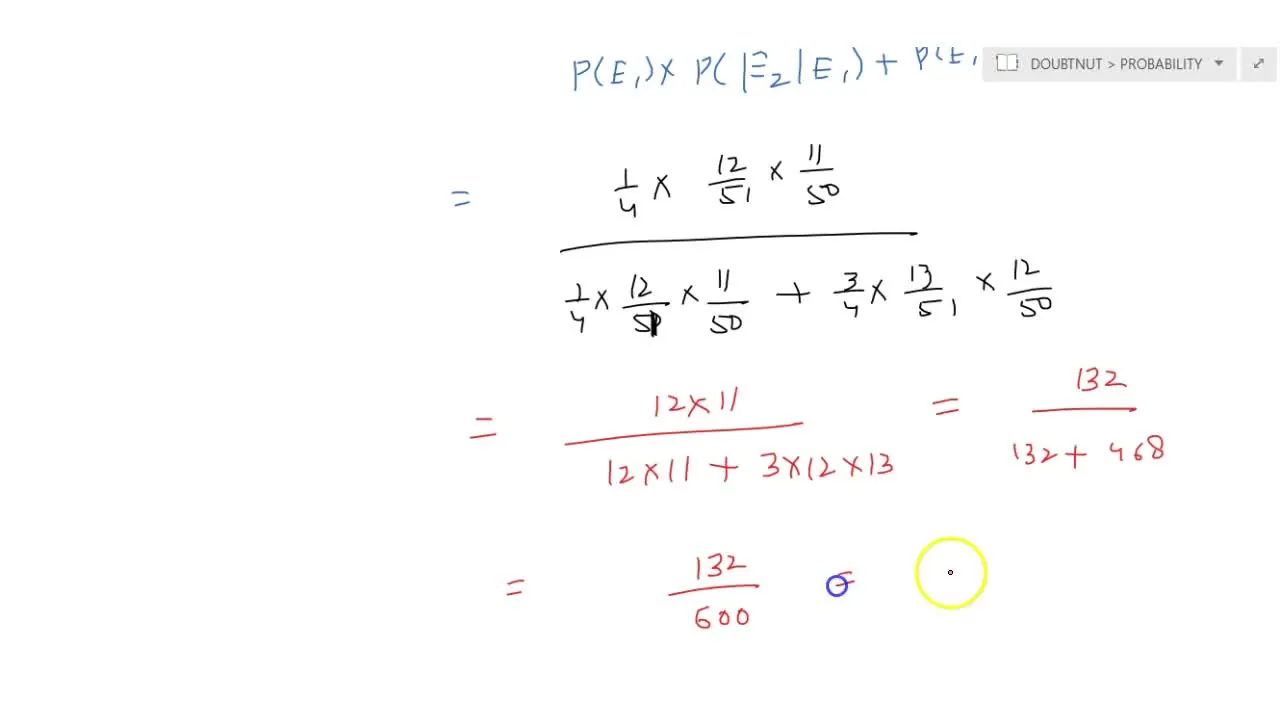
P(BA)=1251⋅1150
P(BA')=1351⋅1250
Now, P(AB)=P(BA).P(A)P(BA).P(A)+P(BA')P(A')
=12⋅1151⋅50⋅1412⋅1151⋅50⋅14+13⋅1251⋅50⋅34
=12⋅11⋅112⋅11⋅1+13⋅12⋅3
=1111+39=1150
Related Playlists
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - Exercise 13.417videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - Solved Examples36videos
PROBABILITY
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.312videos
MATRICES
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.314videos
RELATIONS AND FUNCTIONS
Similar Questions
A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both spades. Find the probability of the lost card being a spade.
View SolutionFind SP when CP = Rs. 56.25 and Gain = 20%.
View SolutionA card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.
View SolutionA card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn at random and are found to be both clubs. Find the probability of the lost card being of clubs.
View SolutionA card from a pack of 52 cards is lost. From the remaining cards of the pack; two cards are drawn and are found to be hearts. Find the probability of the missing card to be a heart.
View SolutionA card from a pack of 52 cards is lost. From the remaining cards of the pack two cards are drawn and found to be hearts. If the probability that lost card is hearts, is k, then the value of 100 k is
View SolutionA card from a pack of 52 cards is lost. From the remaining cards of the pack two cards are drawn and found to be hearts. If the probability that lost card is hearts, is k, then the value of 100 k is:
View SolutionA card from a pack 52 cards is lost. From the remaining cards , two cards are drawn and are found to be speades. Find the probability that missing card is also a spade.
View SolutionA card from a pack of 52 playing cards is lost. From the remaining cards of the pack three cards are drawn at random (without replacement) and are found to be all spades. Find the probability of the lost card being a spade.
View SolutionA card from a pack 52 cards is lost. From the remaining cards , two cards are drawn and are found to be speades. Find the probability that missing card is also a spade.
View Solution