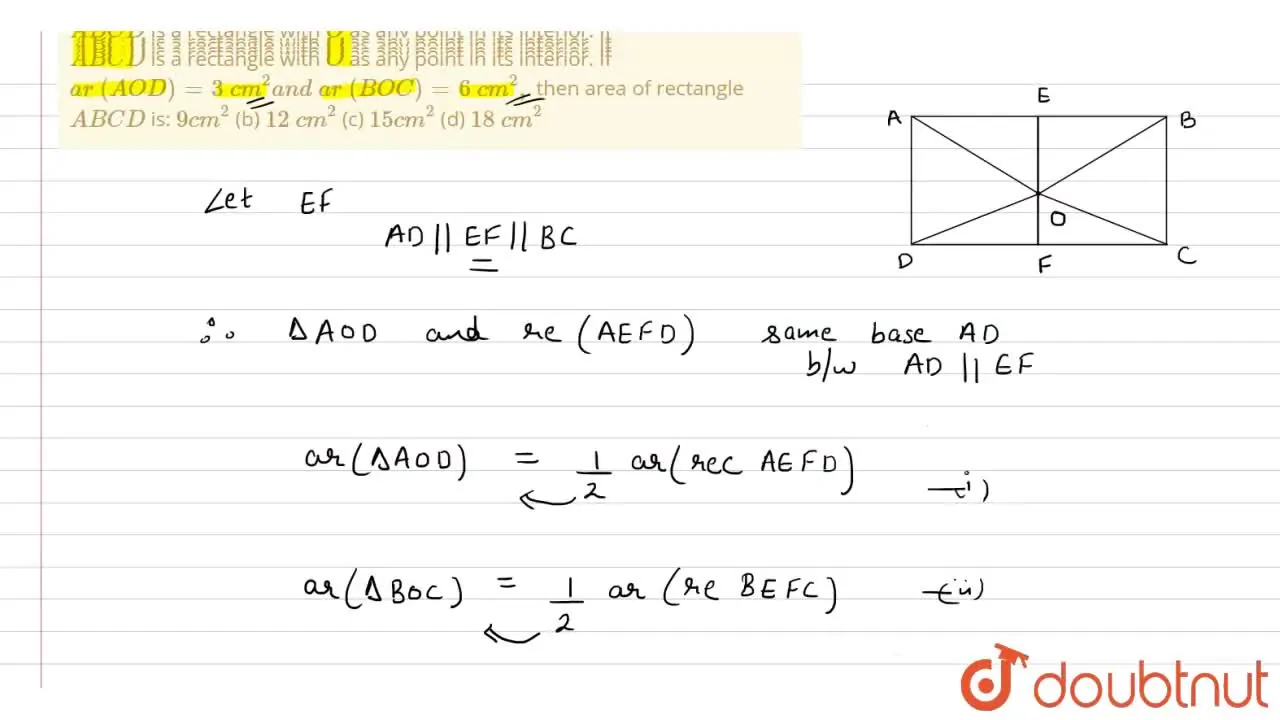
ABCD is a rectangle with O as any point in its interior. If ar (AOD)=3 cm2and ar (BOC)=6 cm2, then area of rectangle ABCD is: 9cm2 (b) 12 cm2 (c) 15cm2 (d) 18 cm2
Step by step video & image solution for A B C D is a rectangle with O as any point in its interior. If a r\ ( A O D)=3\ c m^2a n d\ a r\ ( B O C)=6\ c m^2, then area of rectangle A B C D is: 9c m^2 (b) 12\ c m^2 (c) 15 c m^2 (d) 18\ c m^2 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Related Playlists
Similar Questions
Medians of ABC intersect at G . If ar (ABC)=27 cm2, then ar (BGC)=
(i) 6 cm2
(b) 9 cm2
(c) 12 cm2
(d) 18cm2View SolutionABCD is a parallelogram. P is any point on CD. If ar (DPA)=15 cm2 and ar (APC)=20cm2, then ar (APB)=
(a) 15cm2 (b) 20cm2 (c) 35 cm2 (d) 30cm2View SolutionIf the perimeter of a square is 16 cm, then its area is
(a)4 cm2
(b) 8 cm2
(c)16 cm2
(d) 12 cm2View SolutionThe area of a circle is 220 cm2 . The area of a square inscribed in it is (a) 49 cm2 (b) 70 cm2 (c) 140 cm2 (d) 150 cm2
View SolutionIf the diagonal of a rectangle is 17 cm and its perimeter is 46 cm, the area of the rectangle is (a)100cm2 (b) 110cm2 (c)120 cm2 (d) 240 cm2
View SolutionIn a ABC if D and E are mid-points of BC and AD respectively such that ar (AEC)=4 cm2 , then ar (BEC)=
(b) 4 cm2
(b) 6 cm2
(c) 8 cm2
(d) 12cm2View SolutionABCDEF , ar(ABC)=9cm2 , ar(DEF)=16cm2 . If BC=2.1cm , then the measure of EF is 2.8cm (b) 4.2cm (c) 2.5cm (d) 4.1cm
View SolutionABCD is a trapezium in which AB∣∣DC. If ar(ABD)=24 cm2and AB=8 cm, then height of ABC is 3 cm (b) 4 cm (c) 6 cm (d) 8 cm
View SolutionIn Figure, ABCD and FECG are parallelograms equal in area. If ar (AQE)=12cm2, then arFGBQ=
(a) 12 cm2
(b) 20 cm2
(c) 24 cm2
(d) 36 cm2View SolutionABCD is a parallelogram and O is any point in its interior. Prove that:
(i) ar (AOB)+ar (COD)=12 ar(ABCD)
(ii) ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD)View Solution