Two similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
1:√2
1:2
2:1
√3:1
The correct Answer is:A
To solve the problem step by step, we will analyze the magnetic fields produced by the two coils and find the required ratio.
Step 1: Understand the Configuration
We have two identical coils placed perpendicularly at their centers. Let's denote:
- The current flowing through each coil as I.
- The radius of each coil as R.
- The number of turns in each coil as N.
Step 2: Calculate the Magnetic Field from One Coil
The magnetic field at the center of a single coil is given by the formula:
B=μ0NI2R
Since both coils are identical, we can denote the magnetic field due to the first coil as B1:
B1=μ0NI2R
Step 3: Calculate the Magnetic Field from the Second Coil
Similarly, the magnetic field at the center due to the second coil (which is perpendicular to the first) is also:
B2=μ0NI2R
Since both coils are identical, we have:
B2=B1
Step 4: Determine the Direction of the Magnetic Fields
- Let’s assume the direction of B1 (from the first coil) is upwards.
- The direction of B2 (from the second coil) will be to the right.
Step 5: Calculate the Resultant Magnetic Field
Since B1 and B2 are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field Bnet:
Bnet=√B21+B22
Substituting B2=B1:
Bnet=√B21+B21=√2B21=B1√2
Step 6: Find the Ratio of the Magnetic Fields
We need to find the ratio of the magnetic field due to one coil to the resultant magnetic field:
Ratio=B1Bnet=B1B1√2=1√2
Final Answer
Thus, the ratio of the magnetic field due to one coil to the resultant magnetic field by both coils is:
Ratio=1√2or1:√2
We have two identical coils placed perpendicularly at their centers. Let's denote:
- The current flowing through each coil as I.
- The radius of each coil as R.
- The number of turns in each coil as N.
The magnetic field at the center of a single coil is given by the formula:
B=μ0NI2R
Since both coils are identical, we can denote the magnetic field due to the first coil as B1:
B1=μ0NI2R
Similarly, the magnetic field at the center due to the second coil (which is perpendicular to the first) is also:
B2=μ0NI2R
Since both coils are identical, we have:
B2=B1
- Let’s assume the direction of B1 (from the first coil) is upwards.
- The direction of B2 (from the second coil) will be to the right.
Since B1 and B2 are perpendicular to each other, we can use the Pythagorean theorem to find the resultant magnetic field Bnet:
Bnet=√B21+B22
Substituting B2=B1:
Bnet=√B21+B21=√2B21=B1√2
We need to find the ratio of the magnetic field due to one coil to the resultant magnetic field:
Ratio=B1Bnet=B1B1√2=1√2
Thus, the ratio of the magnetic field due to one coil to the resultant magnetic field by both coils is:
Ratio=1√2or1:√2
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:Subjective type
Explore 10 Videos
- RAY OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:RAY OPTICSExercise:DPP 1.6
Explore 12 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Comprehension Type
Explore 14 Videos
Similar Questions
Magnetic Field due to Circular Coil
View SolutionThe magnetic field at the centre of the current carrying coil is
View SolutionTwo coils are having magnetic field B and 2B at their centres and current i and 2i then the ratio of their radius is
View SolutionTwo circular coils made of similar wires but of radii 20 and 40cm are connected in parallel. Find the ratio of the magnetic fields at their centers.
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
View SolutionTwo identical coils carry equal currents have a common centre and their planes are at right angles to each other. The ratio of the magnitude of the resulatant magnetic field at the centre and the field due to one coil is
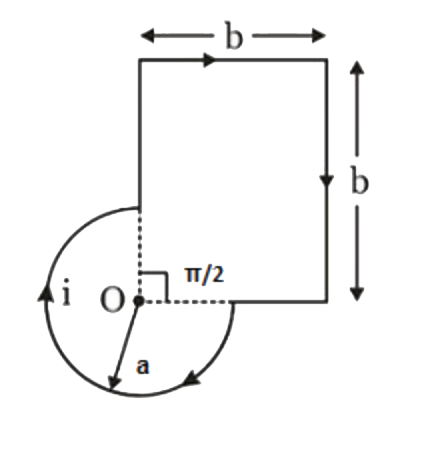
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
View SolutionIf the planes of two identical concentric coils are perpendicular and the magnetic moment of each coil is M, then the resultant magnetic moment of the two coils wil be
View SolutionDiscuss the similarities between the energy stored in the electric field of charged capacitor and the energy stored in the magnetic field of a current-carrying coil.
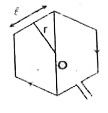
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is
View Solution

