Question

Three particles, each of mass 1gm and carrying a charge q, are suspended from a common point by insulated massless strings, each 100cm long. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side length 3cm, calculate the charge q on each particle.
(Take $g=10m/s^2$).

Answer

A::C

Explanation

Each mass will be in equilibrium under the act of three force namely tension of string, weight, resultant electrostatic force of the two other charges out of these three forces F and mg are perpendicular.


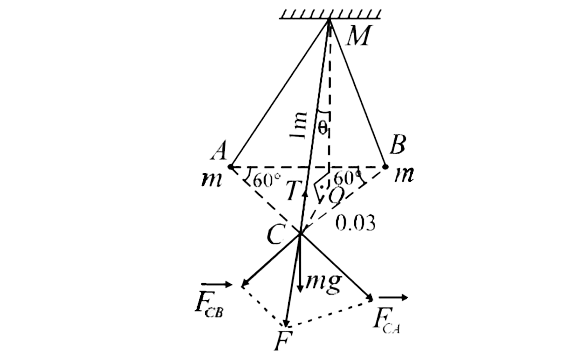
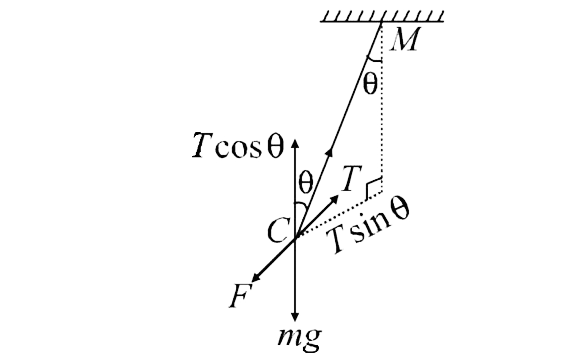
Let T make and angle `theta` with the vertical
`OC=2/3sqrt((0.03)^2-(0.015)^2)=0.0173m`
`:.` `OM=0.9997`
NOTE THIS STEP: Resolving T in the direction of mg and F and applying the condition of equilibrium, we get
`Tcos theta=mg`, `Tsintheta=F`
`:.` `tan theta=(F)/(mg)` ...(i)
`F=sqrt(F_(CA)^2+F_(CB)^2+2F_(CA)F_(CB)cosalpha)`
`:.` `F=sqrt(F_(CA)^2+F_(CA)^2+2F_(CA)^2xx1/2)`
`F=sqrt3F_(CA)=sqrt3xx(kq^2)/((CA)^2)` ...(ii)
[where `F_(CB)=Force on C due to B
F_(CA)=Force on C due to A
`|vecF_(CB)|=|vecF_(CA)|` and `alpha=60^@`]
Also, `tantheta=(OC)/(OM)=(0.0173)/(0.9997)` ...(iii)
From (i), (ii) and (iii)
`(0.0173)/(0.9997)=(sqrt3xx9xx10^9xxq^2)/((0.03)^2xx10^-3xx9.8)`
On solving, we get `q=3.16xx10^-9C`.