There are two blocks of masses m1 and m2,m1 is placed on m2 on a table which is rotating with an angular velocity ω about the vertical axis . The coefficent of friction between the block is μ1 and between m2 and table is μ2(μ1<μ2) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed ω

(a) f1−f1=m2ω2R
f2−f1=m2ω2R
f2=f1+m2ω2R=(m1+m2)ω2R
If there is no sliding between m1andm)=2 therefore
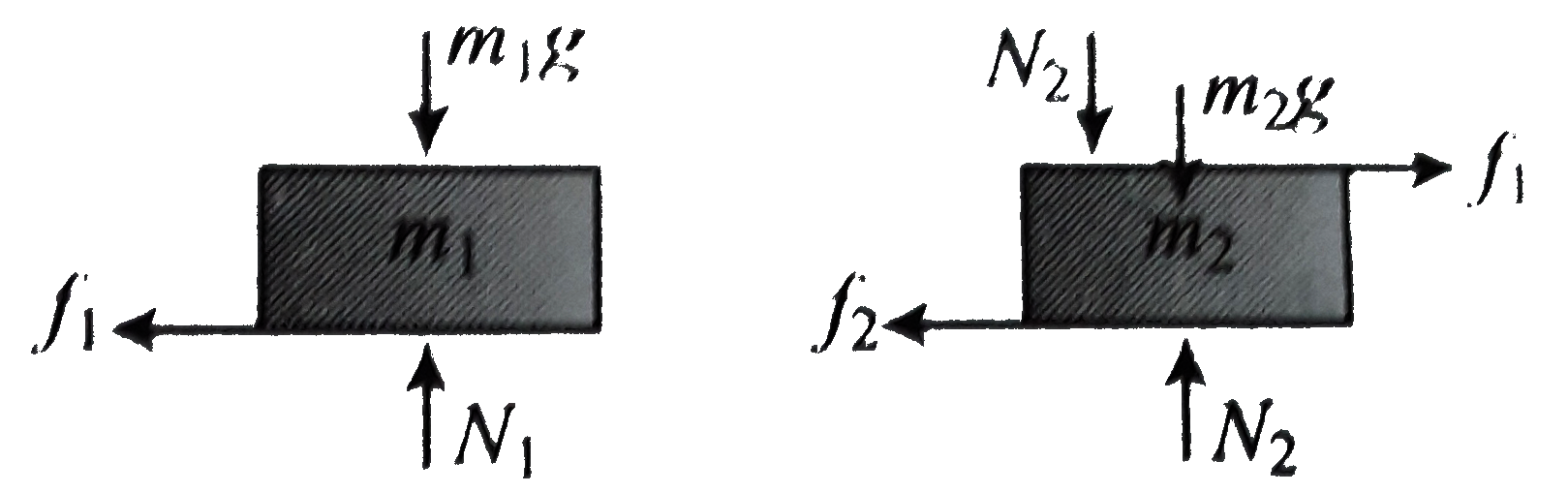
f1≤f1max
m1ω2R≤μ1m1g
⇒ω≤√μ1gR
If there is no sliding between m2 and ground
f2≤μ1N2
(m1+m2)ω2R≤μ2(m1+m2)g
ω≤√μ2gR
As μ1<μ2 hence maximum angular velocity will be √μ1gR
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Subjective
Explore 21 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Single Correct
Explore 87 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Exercise 7.2
Explore 16 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
In fig Block m2 is loaded on block m1 . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block

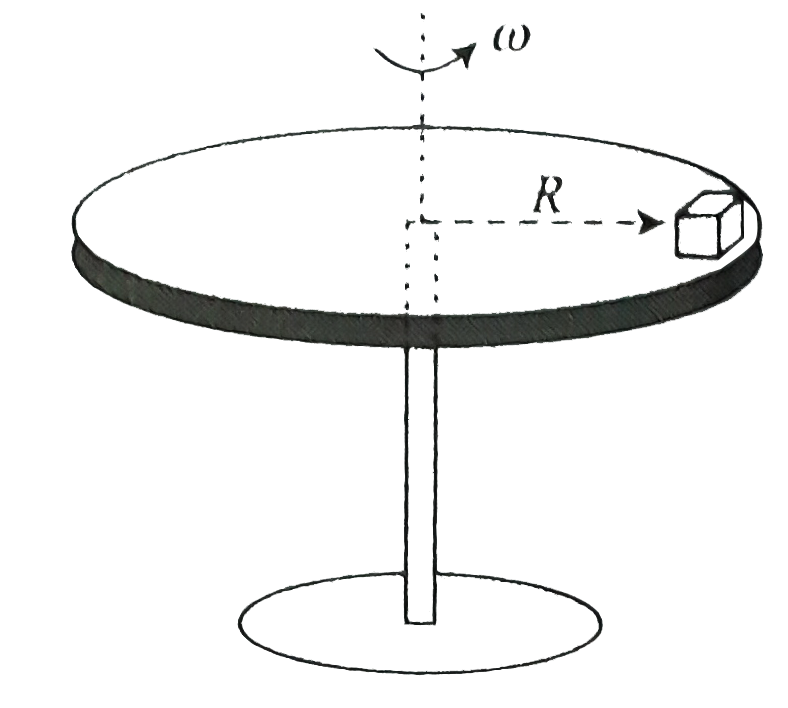
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle ω (along with the block ) about its axis . If coefficient of friction is μ, find the friction force between block and table.
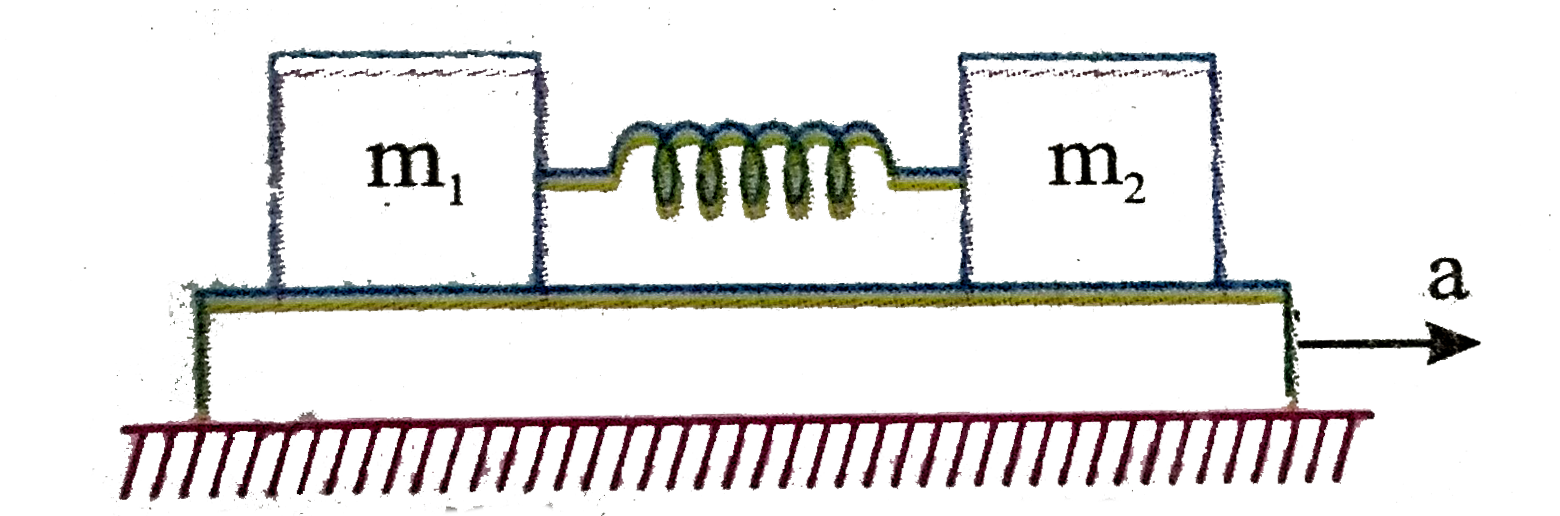
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
View SolutionTwo blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

View SolutionTwo blocks M and m are arranged as shown in the diagram The coefficient of friction between the block is μ1=0.25 and between the ground and M is μ2=13 If M=8kg then find the value of m so that the system will remain at rest

View SolutionTwo blocks of mass m1andm2 lie on smooth horizontal table in contact with each other as shown in figure
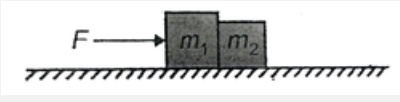
If a force F is applied to the mass m1 then the contact force between the block will be
View SolutionTwo blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is

View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionThe block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block .
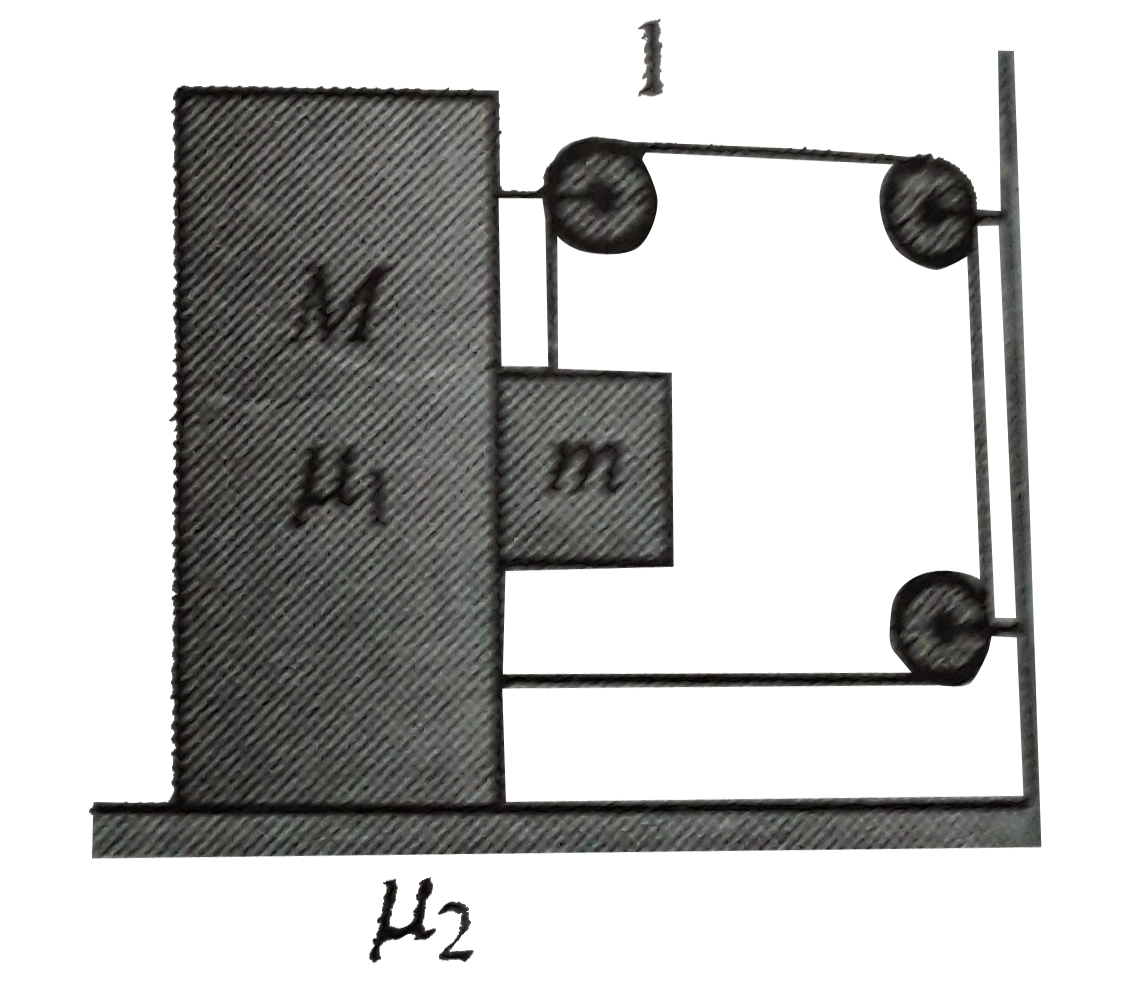
View Solution

