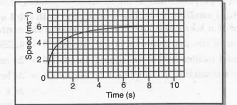
The speed-time graph for a car is shown is Figure

(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during this period.
(b) Which part of the graph represents uniform motion of the car ?
(a) The distance travelled by the car in the first 4 seconds is given by the area between the speed-time curve and the time axis from t = 0 to t = 4 s. This area of the distance-time graph which represents the distance travelled by the car has been shaded in the graph shown on the next page.
In order to find the distance travelled by the car in the first 4 seconds, we have to count the number of squares in the shaded part of the graph and also calculate the distance represented by one square of the graph paper. While counting the number of squares which are half or more than half are counted as complete squares but the squares which are less than half are not counted. When counted in this way, the total number of squares in the shaded part of the graph is found to be 63.

We will now calculate the distance represented by 1 square of the graph. This can be done as follows : If we look at the X-axis, we find that 5 squares on X-axis represent a time of 2 seconds.
Now, 5 squares on X-axis = 2 s
So, 1 square on X-axis = 25 s ...(1)
Again, if we look at the Y-axis, we find that 3 squares on Y-axis represent a speed of 2 m s−1.
Now, 3 squares on Y-axis = 2 m s−1
So, 1 square on Y-axis = 23m s−1 ...(2) ltBrgt Since 1 square on X-axis represents 25 s and 1 square on Y-axis represents 23 m s−1, therefore :
Area of 1 square on graph represents a distance = 25 s×23 m s−1
=415 m
Now, 1 square represents distance = 415 m
So, 63 squares represent distance = 415×63 m
Thus, the car travels a distance of 16.8 metres in the first 4 seconds.
(b) In uniform motion, the speed of car becomes constant. The constant speed is represented by a speed-time graph line which is parallel to the time axis. In the given figure, the straight line graph from t = 6 s to t = 10 s represents the uniform motion of the car. The part of graph representing uniform motion has been labelled AB.
Topper's Solved these Questions
- MOTION Book:LAKHMIR SINGH & MANJIT KAURChapter:MOTION Exercise:QUESTIONS BASED ON HIGH ORDER THINKING SKILLS (HOTS)
Explore 2 Videos
- MODEL TEST PAPER 5Book:LAKHMIR SINGH & MANJIT KAURChapter:MODEL TEST PAPER 5Exercise:Section B
Explore 2 Videos
- SOUNDBook:LAKHMIR SINGH & MANJIT KAURChapter:SOUNDExercise:Value Based Questions
Explore 20 Videos
Similar Questions
The speed-time graph for a car is shown is Figure

(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during this period.
(b) Which part of the graph represents uniform motion of the car ?
View SolutionSpeed - time graph for a car is show in the fig 1.13:Which part of the graph represents uniform motion of the car ?
View Solution
Knowledge Check
The distance- time graph of a body is as shown in the figure. The part of the graph that represent the unifrom speed of the body is
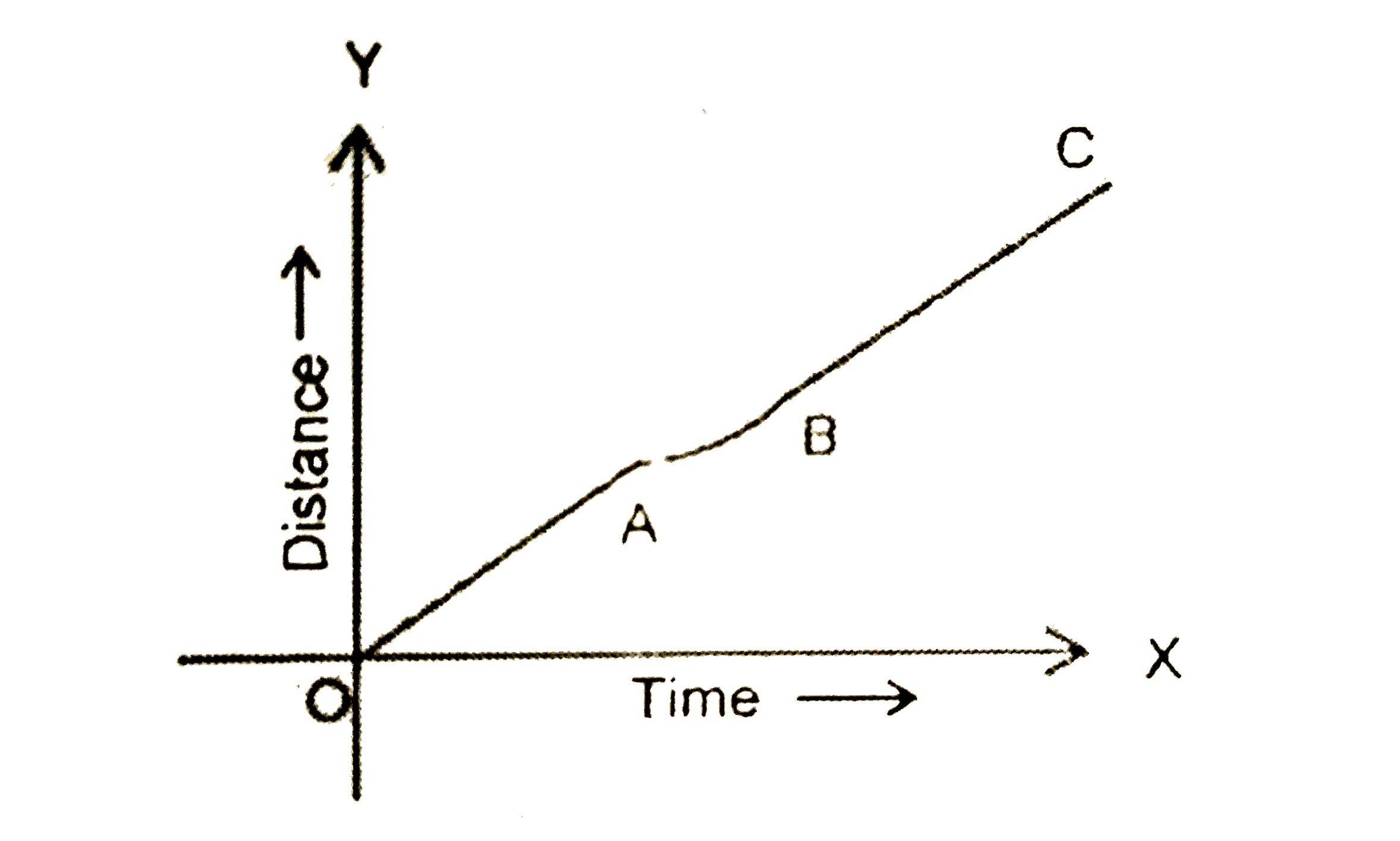 AOABABCBCDBoth OA and BC
AOABABCBCDBoth OA and BCThe graph given here shows a car following the linear path with uniform speed. Study the graph and answer the questions.
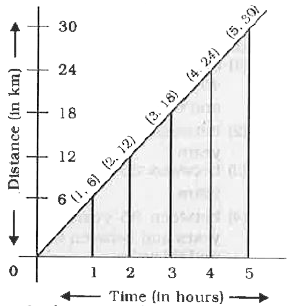
The distance travelled by the car in 4.5 hours isA27 kmB30 kmC36 kmD40 kmThe distance- time graph of a body is as shown in the figure. The part of the graph that represent the unifrom speed of the body is
 AOABABCBCDBoth OA and BC
AOABABCBCDBoth OA and BC
The distance versus time graph of a car is shown in the given figure.
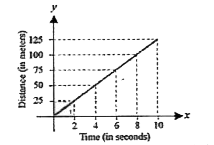
View SolutionThe diameter of a wheel of a car is 63 cm. Find the distance travelled by the car during the period in which the wheel makes 1000 revolutions.
View SolutionSpeed time graph of a particle shown in figure. Find distance travelled by particle in 5second.
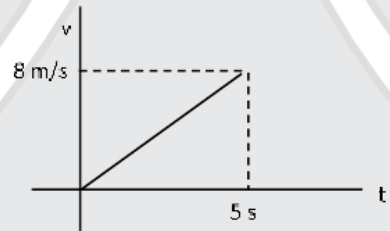
View SolutionThe speed of a car as a function of time is shown in figure.
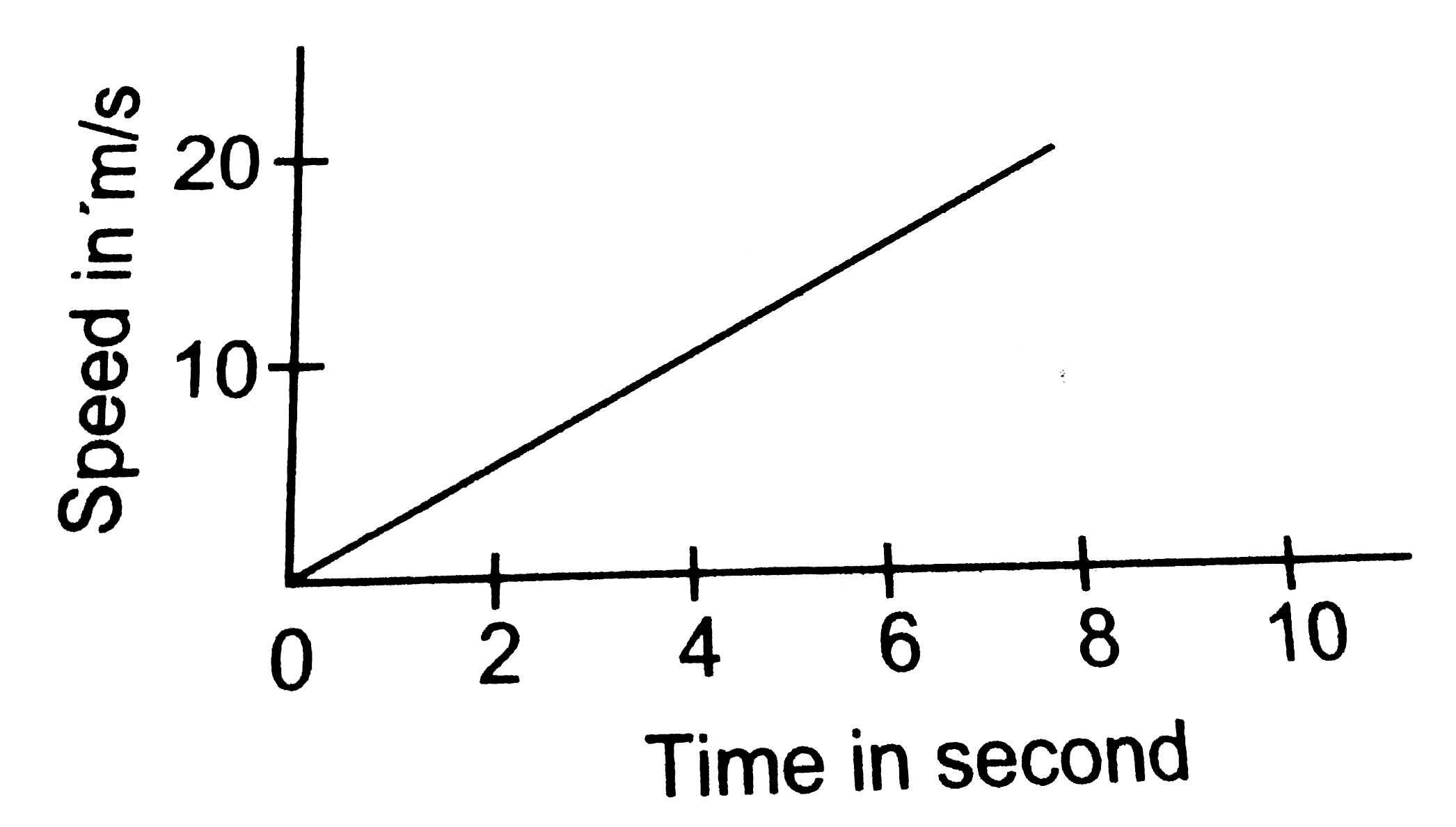
Find the distance travelled by the car in 8 seconds and its acceleration.
View SolutionThe diameter of a wheel of a car is 63 cm. Find the distance travelled by the car during the period, the wheel makes 1000 revolutions.
View Solution
