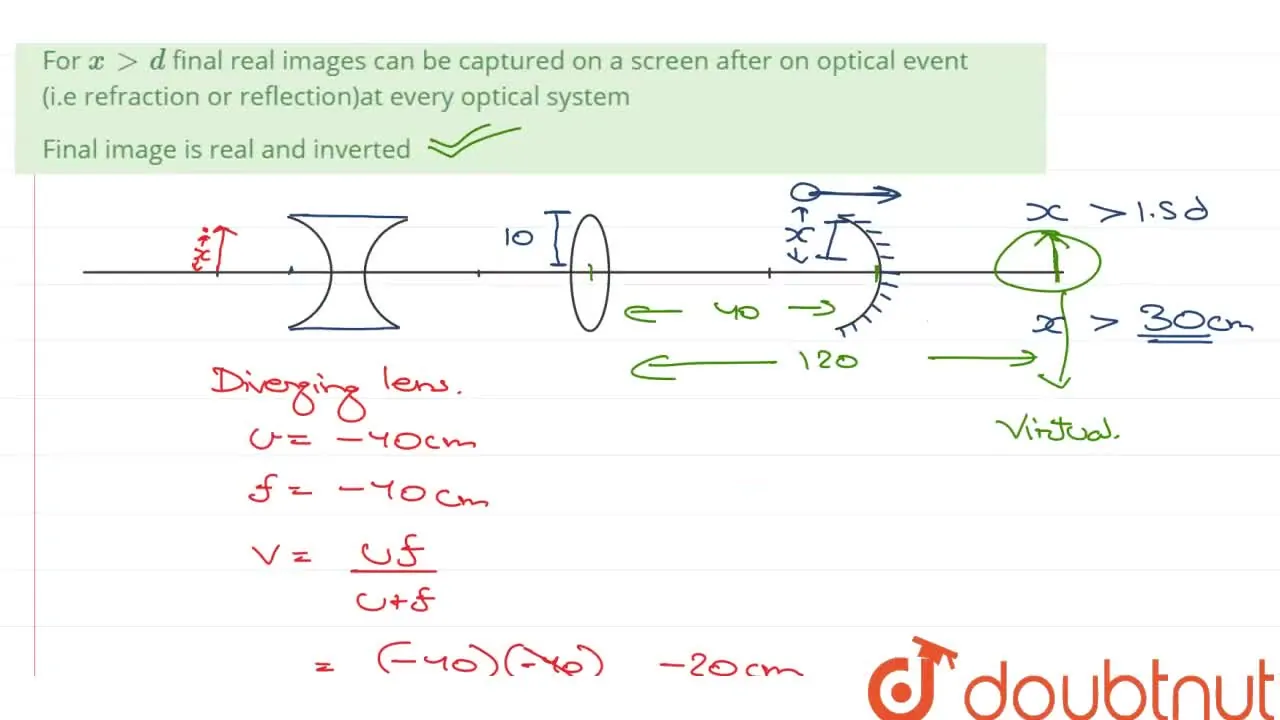
The following objects are placed one after each other in given order onto a central axis with a separation of 40 cm each. A point source of light O. a diverging lens of focal length 40 cm. a converging lens of focal length 40 cm and converging mirror of focal length 80 cm. The aperture diameter of lenses and mirror is d=20 cm. If a point source of light is placed at a perpendicular distance of x from central axis then. (You have to consider single optical event at any optical element)
Mark the CORRECT statement(s):-
Final image is formed in the plane of converging lens
If x>1.5d the rays will not be reflected by converging mirror
For x>d final real images can be captured on a screen after on optical event (i.e refraction or reflection)at every optical system
Final image is real and inverted
The correct Answer is:A, C, D
Let us follow the way the images are formed by the lenses and the mirror. The virtual image formed by the diverging lens has an image distance of
i1=O1f1O1−f1=−4.44−(−4)dm=−2dm (dmrarrdecimeter)
Since the linear magnification is
m1=Hi1HO1=i1O1=12
the height of the first image is
Hi1=x2=HO2.
This virtual image is seen by the diverging lens as an object with an object distance of O2=f2+|i2|=6dm, therefore the image formed by second lens has an image distance of
i2=O2f2O2−f2=6.46−4dm=12dm
The linear magnification of the second lens is
m2=i2O2=126=2
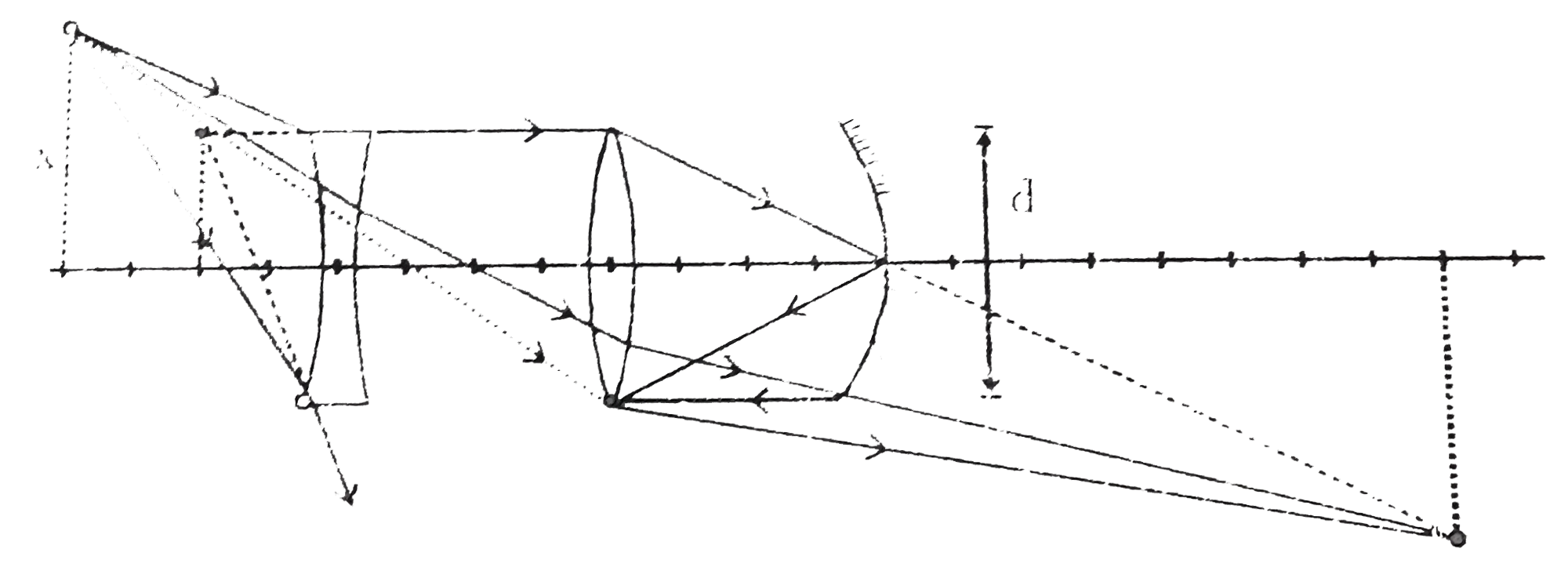
Hence the height of the second image is Hi2=m2HO2=m2Hi1=xc=HO3.
The second image is seen by the concave mirror as a virtual object bering at a distance of O3=f3−i2=−8dm, therefore the image is formed at
i3=O3f3O3−f3=−8.8−8−8=−64−16=1dm
This is a real image and since the linear magnification of the mirror is:
m3=i3O3=12
the height of the final image is
Hi3=m3HO3=x2
Note that final image is formed in the plane of the converging lens, therefore the image can only be captured on a screen if its height is greater than the radius of the lens. This happens when x is greater than d, therefore the list condition for perpendicular is d lt x. If x is increased further than 1.5d, the rays will all pass under the concave mirror and there will be no image formation. Therefore the solution of the problem is :
d<x<1.5d.creased further than 1.5d, the rays will all pass under the concave mirror and there will be no images formation. Therefore the solution of the problem is:
d<x<1.5d.
Related Playlists
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS17videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS14videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics71videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS44videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
A converging lens of focal length 40 cm is kept in contact with a diverging lens of focal length 30 cm. Find the focal length of the combination.
View SolutionAn object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
View SolutionA converging lens of focal length 5.0cm is placed in contact
with a diverging lens of focal length 10.0cm. Find the combined focal length of
the system.View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by a mirror is
View SolutionA converging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed 60 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 50 cm from the lens. Find the locations of the images formed.
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
View SolutionA convex lens of focal length 20 cm is placed in front of a convex mirror of focal length 15 cm at a distance of 5 cm. An object of length 2 cm is placed perpendicular to the common axis at a distance of 20 cm from the lens
View SolutionA diverging lens of focal length 20 cm and a converging mirror of focal length 10 cm are placed coaxially at a separation of 5 cm. Where should an object be placed so that a real image is formed at the object itself ?
View SolutionThe radius of curvature of a plane mirror of focal length 40cm is :
View Solution