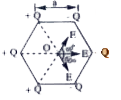
Six charges are placed at the vertices of a regular hexagon as shown in the figure. The electric field on the line passing through point O and perpendicular to the plane of the figure at a distance of x ( >> a) from O is
1) Qaπε0x3 2) 2Qaπε0x3
3) √3Qaπε0x2 4) zero.

This is basically a problem of finding the electric field due to three dipoles. The dipole moment of each dipole is P = Q(2a)
Electric field due to each dipole will be E=KPx3.
The direction of electric field due to each dipole is as shown below:
Enet=E+2Ecos60∘=2E
=2(14πε0)(2Qax3)=Qaπε0x3.
Similar Questions
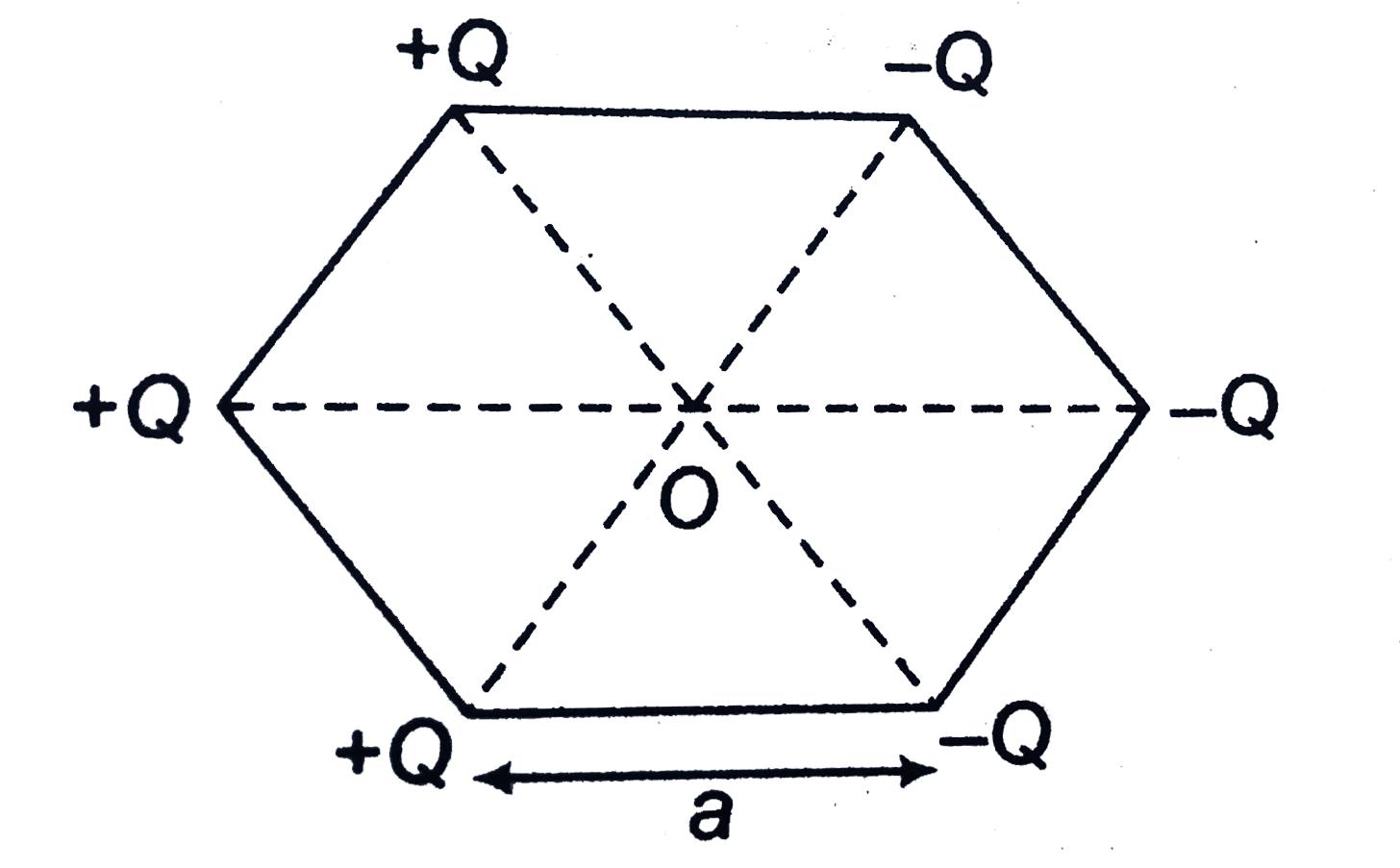
Six charges are placed at the vertices of a rectangular hexagon as shown in the figure. The electric field on the line passing through point O and perpendicular to the plane of the figure as a function of distance x from point O is (assume x>>>a)
View SolutionThe line passing through the point -1, 2, 3 and perpendicular to the plane x - 2y + 3z + 5 = 0 will be
View Solution
Knowledge Check
Six charges are placed at the vertices of a rectangular hexagon as shown in the figure. The electric field on the line passing through point O and perpendicular to the plane of the figure as a function of distance x from point O is (x>>a)
 A0BQaπε0x3C2Qaπε0x3D√3Qaπε0x3
A0BQaπε0x3C2Qaπε0x3D√3Qaπε0x3Electric potential due to a dipole at a position →r from its centre is: where (K=14πε0
AK→p.→rr3BK.→p.→rr2CK.→P×→rr3DK.→p×→rr2
41.Self energy of conducting sphere of radius r carrying charge is (1) Q28πε0(r) (2) Q24πε0(r) (3) Q26πε0(r) (4) Q22πε0(r)
View SolutionThree charges are arranged on vertices of an equilateral triangle "ABC" of side "a" as shown.The magnitude of electric field of point "P" on the angular bisector of "A" and at a distance "d" from "A(d>>a) is qa√xyɛ0πd3 where "x" and "y" are co-prime. Value of (xy)2 is equal to
View SolutionSix point charges (each of magnitude Q) are placed on the six vertices of a cube of side x such that two adjacent vertices are vacant. Electrostatic field intensity at the centre of the cube is (k=14πε0)
View SolutionElectric potential due to a dipole at a position →r from its centre is: where (K=14πε0
View SolutionA short electric dipole having dipole moment ¯ρ is placed along x-axis as shown in figure. The electric potential at point A(-2, 3) is (k=14πε0 and all quantities are in S. I. units)
View SolutionIf the elctron ( charge of each electron =−e) are shifted by a small distance x,a net +ve charge density ( per unit area ) is induced on the surface. This will result in an electric field E=nex/ε0 in the direction of x and a restoring force on an electron of
−ne2xε0,
Thus m..x=−ne2xε0
or ..x+ne2mε0x=0
This gives ωp=√ne2mε0=1.645×1016s−1
as the plasma frequency for the problem,.
View Solution

