One mole of an ideal gas with adiabatic exponent γ undergoes the process
(a) P=P0+αV
(b) T=T0+αV
Find Molar heat capacity of the gas as a function of its volume.
From first law dQ=dU=dW
nCdT=nCVdT+PdV
C=CV+PndVdT
(a) P=P0+αV
nRTV=P0+αV
nRT=P0V+α
nRdT=P0dV+0
dVdT=nRP0
C=CV+PndVdT
=Rγ−1+(P0+αV)n.nRP0
=Rγ−1+(P0+αV)RP0
=Rγ−1+R+αRVP0
=γRγ−1+αRVP0
(b) T=T0+αV
dT=αdV⇒dVdT=1α
C=CV+PndVdT
=Rγ−1+RTV.1α
=Rγ−1+RαV(T0+αV)
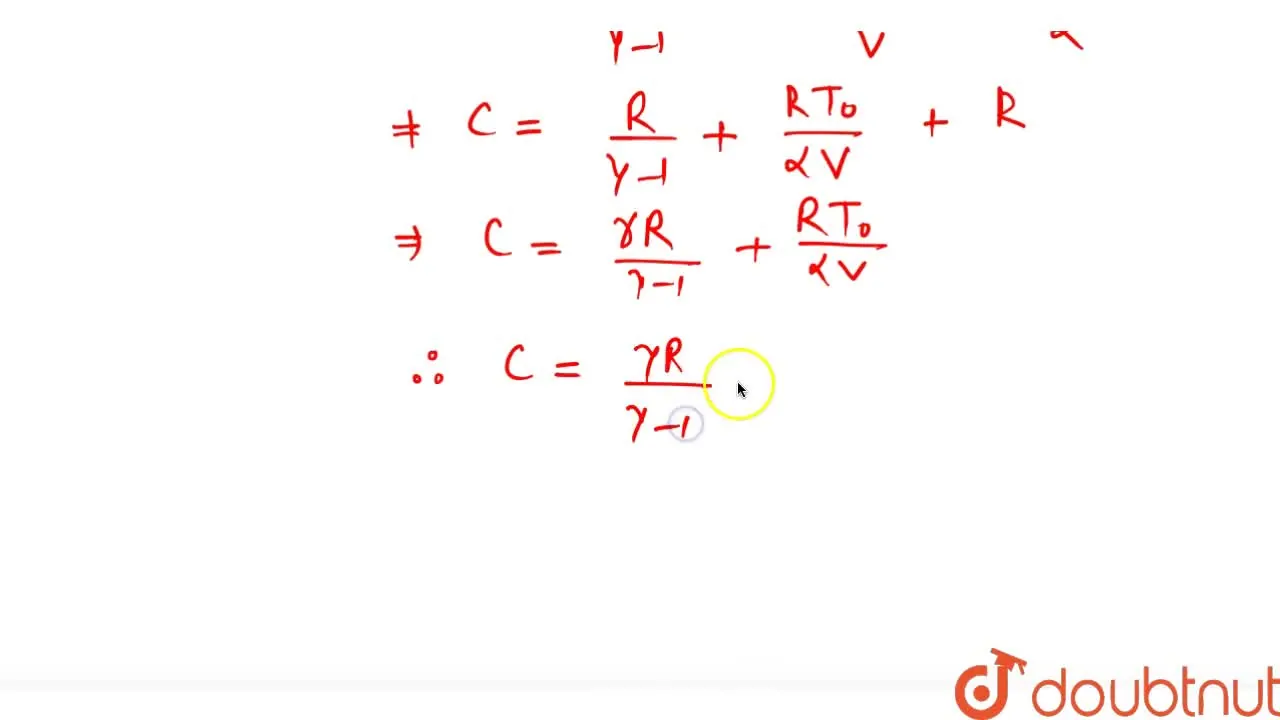
=Rγ−1+RT0αV+R
=γRγ−1+RT0αV
Related Playlists
Similar Questions
One mole an ideal gas whose adiabatic exponent equals γ undergoes a process p=p0+α/V, where p0 and α are positive constants. Find :
(a) heat capacity of the gas as a function of its volume ,
(b) the internal energy of heat transferred to the gas, of its volume increased from V1 to V2.View SolutionOne mole of an ideal gas with heat capacity at constant pressure Cp undergoes the process T=T0+αV, where T0 and α are constants. Find :
(a) heat capacity of the gas as a function of its volume ,
(b) the amount of heat transferred to the gas, if its volume increased from V1 to V2.View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionThe molar heat capacity for a gas at constant T and P is
View SolutionAn ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
View SolutionOne mole of an ideal monoatomic gas undergoes the process T=T0+4V, where T0 is initial temperature. Find
(i) Heat capacity of gas as function of its volume.
(ii) The amount of heat transferred to gas if its volume increases from V0 to 4V0.View SolutionFind the molar heat capacity of an ideal gas with adiabatic exponent γ for the polytorpic process PVn= Constant.
View SolutionOne mole of an ideal monatomic gas undergoes the process P=αT1/2, where α is constant . If molar heat capacity of the gas is βR1 when R = gas constant then find the value of β.
View SolutionAn ideal gas is made to undergo a process T=T0eαV where T0 and α are constants. Find the molar specific heat capacity of the gas in the process if its molar specific heat capacity at constant volume is Cv. Express your answer as a function of volume (V).
View SolutionAn ideal gas with the adiabatic exponent γ goes through a process p=p0−αV, where p0 and α are positive constants, and V is the volume. At what volume will the gas entropy have the maximum value ?
View Solution